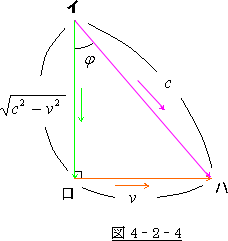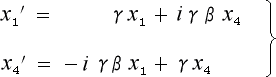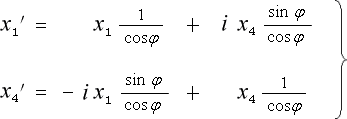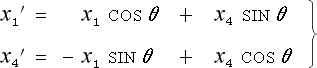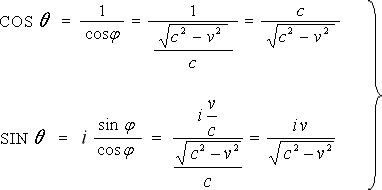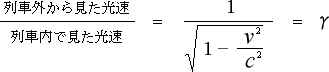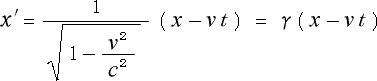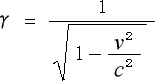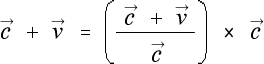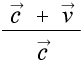（２）三角関数の本当の意味
(a) 列車内で見た光と外から見た光との関係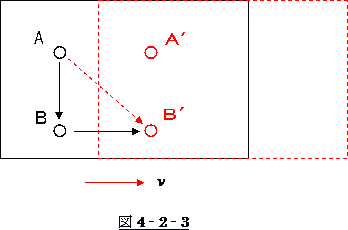
ここでは、まず、第一章で使った
「列車の中の時間の矛盾」の話を引用します。
右図は、列車の中の様子を示した物です。
Ａ，Ｂは座席の位置です。列車は速度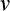 
で右
方向に動いている物とします。
ここで、Ａの座席の人が煙草を吸う為に、ライター
で火を点けたとしましょう
そうすると、その光はＢの人には、まっすぐＡ→Ｂの方向へ来た様に見えます。
ところが、この光景を外から見ていた人には、光はＡ→Ｂ′の方向へ来た様に見えます。
光がいくら速いとは言え、ＡからＢに届く間に列車も少しは前に動いているからです。
その様子は、図4‐2‐3の三角形で表されます。
これは列車の中で見た光の行跡と、それを列車の外から見た場合の光の行跡と、列車の移動
との関係を表した物です。 この三角形を速度の関係で見直してみましょう。
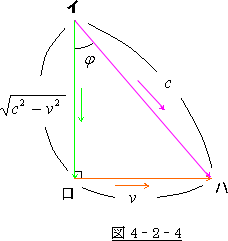
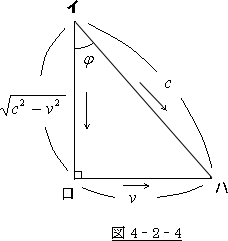
そうすると、それは、図 4‐2‐4 の様になります。
相対論では、列車の中の光の速度も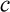 
なのですがそれを無視して
三角形だけで考えてみますと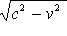 
になります。
この図は何となく 図 4‐2‐2 に似ているでしょう。
あちらの方は、間違っていたのだから、こっちの方が本物という
事になります。
(b) こじつけた cosθ は本当は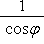 
で sinθ は本当は i 
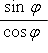だった
ここで、図 4‐2‐4 より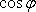 
, 
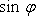を求めてみましょう。
そうすると
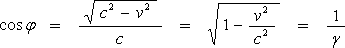(4-2-3)
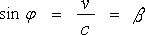(4-2-4)
となりまして、座標変換の時にこじつけた物と、何かしら似た物が出て来ます。同じではありませんが。
次に、これを（4-1-10) 式
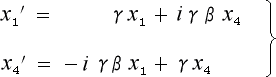(4-1-10)
に代入してみましょう。 そうすると
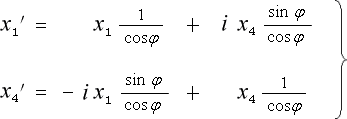(4-2-5)
となりまして、これも何かしら座標の回転の式と似た形になります。しかし同じではありません。
ここで、この式の 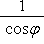を ＣＯＳθ に i 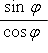を ＳＩＮθ に置き換えてみましょう。
そうすると
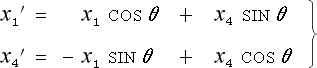(4-2-6)
となりまして座標の回転の式や（4-1-11) 式とそっくりになります。
しかしながら、これは 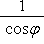を ＣＯＳθ に i 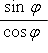を ＳＩＮθ に置き換えた物ですから、正しくはありません。
次は、このＣＯＳθとＳＩＮθを、 (4-2-2) 式を作ったのと同じやり方で、簡単な式に直してみましょう。
そうすると
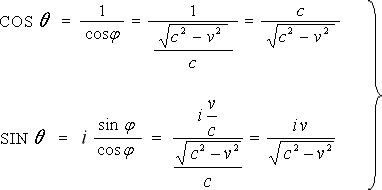(4-2-7)
となりまして(4-2-2)式と全く同じ結果になります。
つまり、座標の回転の所でこじつけた cosθ・ sinθ とは、
実は (4-2-6) 式の ＣＯＳθ・ＳＩＮθ の事だったのです。
cosθ にこじつけた (4-1-10) 式の γ とは、実は図4‐2‐4 の中の 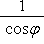の事であり、
sinθ にこじつけた iγβ とは、実は図4‐2‐4の中の i 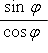の事だったのです。
座標の回転の所で、γ や iγβを三角関数としてこじつけたとしても、曲がりなりにも成り立って
いたのは、こういった裏付けが有ったからです。
それを、アインシュタインかミンコフスキーかは知りませんが、早とちりして座標の回転だとか・
時空の転換などと、とんでもない方向へと発展させて行ったのです。
これは、そんな大層な物ではありません。
単に、「《動いている系の速度》と《動いている系内で見た光の速度》と、《それを外から見た場合の
光の速度》との関係」を表しているだけですから。
(c) γ は相対論の矛盾を調整する係数
図4‐2‐4では、列車の外から見た光の速度を 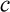，列車の速度
を 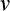としている為、直角三角形を作る便宜上、列車の中での光の
速度を 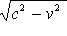としましたが、これは、第二章第二節（4）の
「動く時計の遅れ」や第三章第一節（2）の（ｂ）の「アインシュ
タインのローレンツ変換の誘導」の所でも懸案として残しておいた
事です。
そこで、ここでは、これについて、考えてみる事にしましょう。
まずは、列車の中で見た光の速度と、それを外から見た場合の光の速度の比を取ってみます。
そうすると
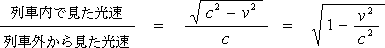(4-2-8)
になります。これは何かと言うと、言わずと知れたローレンツ変換の分母です。
そして、これをひっくり返しますと
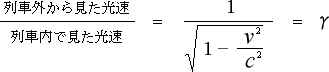(4-2-9)
と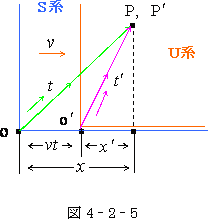
なりまして、ローレンツ変換の γ になります。
さて、ここでちょっと 図 4‐2‐5 を見て下さい。
これはローレンツ変換を求める時に使う図で、動いている系と
静止している系の関係を表している物です。
系 は Ｓ系 に対して速度 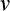で 
軸方向を右に動いている
物とします。
(注； t ＝ t′＝ 0 のとき、O と O′は重なっている物とする)
この図から単純に 
の距離を求めますと
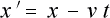(4-2-10)
になります。ところが、ローレンツ変換では
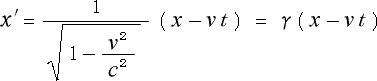
となっていまして、ここには
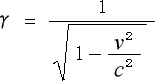
という、わけの分からない係数がついていました。
最初は、これが何を意味するのか良く判りませんでした。 しかし、これが
いう事でしたなら、何となく、その意味する所が解る様な気がします。
つまり、これは、相対論の矛盾を調整する係数だからです。
相対論以前の考え方でしたなら、列車の中で発した光の速度を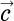 
、列車の速度を 
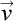としますと、
外から見た光の速度は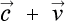 
となります。 （注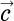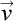； 、 はベクトル）
ところが、相対論では列車の中で見た光速も外から見た光速も同じですから
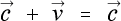(4-2-11)
としなければなりません。しかし、これは、論理的に矛盾します。
こういう矛盾を調整する為に、式はどういう手段を採ったか、 それは
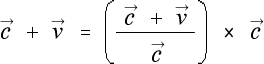
となるようにした事でしょう。こうすれば問題は消せます
ところで
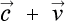； 列車の外から見た光速
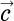； 列車の中で見た光速
ですから
となり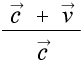 
は γ と同じ意味になります。
そういう事から、ローレンツ変換の
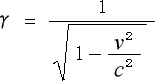
は、相対論の無理・矛盾を調整する係数とみなせるわけです。
式は多分こういう係数を掛ける事によって矛盾を調整していたのでしょう。
その事から、逆に“列車の中で見る光の速度と、それを、外から見た場合の光の速度とは、
本来、違うのだ”という事が判って来ます。
アイシュタインは、原則的に
「静止系から見ても、運動系から見ても光速は同じ」
としながら、理論誘導の所では
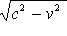「運動系の 軸に垂直に発した光を静止系から見ると、その速度は になる」
等とやっていました。
我々、素人から見れば「何それ、そんなの有り！？」ですが、
本人は、無頓着というか、融通無碍というか、相反する事を平気でやっていました。
そんな事をすれば、どんな奇想天外な理論でも創れるでしょう。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る