(a)
, 
は距離であって座標ではない。
時空の転換の間違いは、はっきりしましたが、実は、それ以前の問題として、四次元座標の間違いが
あります。 話の流れ上、回転座標の方を先にやりましたが、実は、こっちの方が、より基本的な問題
だったのです。
, は距離であって座標ではない。 相対論では 式（4-1-5)
の , を勝手に座標と見なし、
と置き換えて四次元座標にしていますが、これは間違っています。
の元の式は
でした。
これは、ローレンツ変換の説明の所でも詳しく述べました様に、距離の式です。
ですから。
この式の , は全て距離なのです。
座標などではありません。
もちろん、 については座標と見なす事も出来ますが、
は、そうは行きません。これは明白に距離ですから。
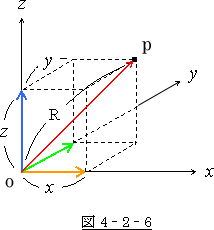
は 図 4‐2‐6 の中で光が走った所の O P 間の距離です。
この式の本当の意味は、
距離 OＰの 
軸方向成分の二乗と
距離 OＰの 
軸方向成分の二乗と
距離 OＰの 
軸方向成分の二乗とを
加えた物は、光が速度 
で 
時間掛けて走った所の距離 OＰ の二乗に等しい
という事だけです。
これは、単なる距離の関係式です。
この式は、「右辺も左辺も距離という点で等価だ」と言ってるだけでして、けっして
「左辺が座標で右辺が時刻、そして両者が等価」等と、たわけた事を言っているわけ
ではありません。
それを、何を勘違いしたのか を座標、 を時刻と思い込んで
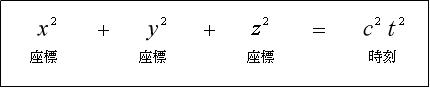
と置き
と変化させて、無理やり四次元座標に持って行きました。
その結果、《空間次元と時間次元とが等価で交換可能》という、
とんでもない勘違いの世界へと、引っぱって行ったのです。
本当は、単に《右辺も左辺も距離という点で等価》という事だけだったのですが。
この式は
までに留めるべきです。これを
とすれば間違いになります。 この場合は
とおくのが正しいのです。
この 
の前のマイナス記号まで の範囲に入れて 
とするのは、数学上の
テクニックでは可能でも、こんな所で使ってよいわけはありません。
これは、道理を無視した滅茶苦茶なやり方です。
そんな事をすると、物事の本質を見誤る事になります。
これを国語の文章問題に例えるなら
「僕は、知らない」とする所を、句読点を一つずらして、
ボク シ
「僕、 走らない」とする様な物です。 また
ボク ハシ
「木 柱 無い」とする事も出来ます。 そして、これを
ボク ハシラ ナ
「木 柱 無い」と読み換える事も出来ましょう。
モク チュウ ナ
言葉遊びならともかく、大事な文章でこんな事は許されません。
外交文書なら、戦争になりかねません。
しかるに相対論では、こういう滅茶苦茶を随所でやっているのです。
「同時性」や「ローレンツ収縮」・「時間の遅れ」・「時空の転換」等も、所詮はパソコンの
変換ミスみたいな物でしょう。
人々は、変換ミスの結果出来上がった文章を、「奇想天外だ！」、「不可解だ」、「素晴らしい」、
「馬鹿げている」等と議論し合っているようなものです。
式（4-1-4)
の中の は座標ではなく距離である事は、はっきりしました。
しかし、それにも関わらず が 三次元空間の基本座標でもあり基本次元でもある事に
変わりはありません。
また一方で座標は原点からの距離で表わされます。
その事から 「座標」＝「距離」と思い込んでおられる方も多いでしょう。
その為、距離 もまた座標に出来るのではと、お思いの方があるかも知れません。
相対論はその思いをそのまま式にしました。
しかし、その思いつきは余りにも安易でした。
を座標にしようと思えば出来ないことはありません。
が、しかし、それは三次元空間内の座標になるだけでして
軸や 軸・ 軸から独立した第四の座標軸を持つ座
標や次元になるわけではありません。
ここからは その説明です
その為には、まず、(4-1-3) 式の
(4-1-3)
と図 4‐2‐6 を用いる事にします。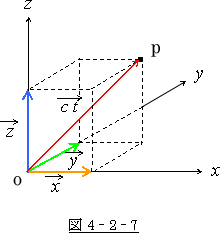
そして次には、
これをベクトルに置き換えます。
そうすると、式(4-1-3) は
となり、
図 4‐2‐6 は図 4‐2‐7 の様な形に置き換えられます。
四番目の座標に相当する はベクトルでは 
です。
図と式から明らかな様に は 
の合成です。
は、それぞれ独自の座標軸を持ち、独自の方向次元を持っています。
従って、他の座標軸からも独立しています。
ところが は、これら の合成ですから、 軸・ 軸・ 軸から独立していません。
故に、第四の座標・次元たり得ません。
そもそも、独立した座標・次元というものは、他の座標・次元に関係なく独自の値をとれるものです。
例えば、 は や がどんな値であろうと関係なく、 軸上に自由に値がとれます。 , も
同様です。
ところが、 はそうは行きません。 は の値に拘束されます。
の値が決まれば、 の値は一つに固定されます。
そして のどれか が動けば、連動して も動かされます。
従って、 に自由度は有りません。
「そうは言うが、 の方を変える事だって出来るではないか。
そうすれば に自由度はある事になる」とおっしゃる方があるかも知れません。
ところが、 を変えると OＰ 間の距離が動きますので、 も連動して動かされます。
従って、 に自由度はありません。 は から独立していないのです。
故に、第四の座標・次元たり得ません。
そういうわけで、四番目の座標・次元は存在しません。
だけなら時間次元として空間次元とは別個に次元が考えられますが、 となれば距離ですから
話は別です。
これは時間の次元ではありません。距離の次元なのです。
それでも、まだ、御不満の方もあろうかと思われます
ので、今度は を座標にして勘違いの世界から目を
さまして頂こうと思います。
の 
を座標にする場合、これまで
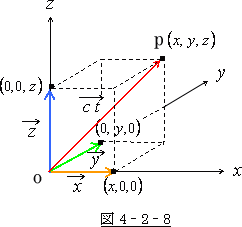
の先端の座標を座標にしていました。従って、そのやり方で行けば
の座標は の先端の座標、つまりＰ点の座標という事になります。
そうすると、 の座標は () という事になるのです。
もっとも、これでは、他の座標とのつりあいが取れませんので、他の座標も修正して
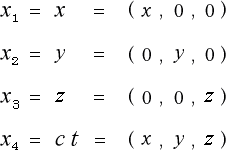
として置きましょう。そうすると、バランスがとれて
としても、おかしく無くなります。
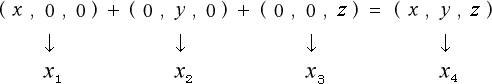
ですから
この時、始めて、距離の式やベクトルの式との間に整合性が取れて来ます。
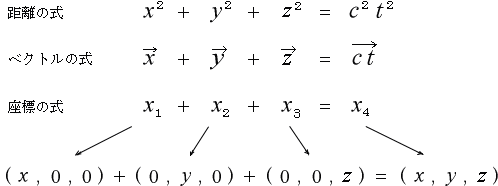
という様に
そして、それぞれの式が関連性を持ち、式の間に一貫性が出て来ます。
を座標にするとは、実は、こういう事だったのです。
別に“四次元空間になる”等と言う、大それた物ではありませんでした。
というわけで、 
こと は 軸・ 軸・ 軸から独立した第４の座標・次元とはなりません。
四次元座標では ＝ 等として、虚数を用いる事により、あたかも、 軸, 軸, 軸に
直交する第四の座標軸でも存在するかの如く錯覚させていますが、これは間違いです。
読み物的相対論の本では、四次元時空は図 4‐2‐9 の様な形で表わされ、
物理学の本では図 4‐2‐10 の様な形で表わされます。
どちらも空間軸に直交する形で時間軸が示されています。
図 4‐2‐10 では空間軸が 軸しか書いてありませんが、これは、四次元全部を図で表わす事が
出来ないので、 軸で代表してあるだけです。
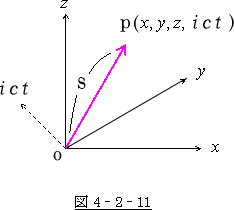ちなみに、私が大学で講義を受けた時の図は図 4‐2‐11でした。
ここでは、あくまでも、 軸は 軸, 軸, 軸に直交する
軸として考えられています。
しかしながら、式の成立過程に立ち戻れば、そうでない事は明白と
なるでしょう。
それにもし、仮に、空間が図4‐2‐11の様な座標空間でした
なら、OＰ間の距離 
を求める場合、不都合を生じます。
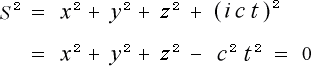(4-2-12)
となるからです。これでは距離 は 0 になってしまいます。
ここ四次元時空の所では、相対論を創った時の元の式が
だった事を忘れているかの様です。
それどころか、相対論 (教科書『物理学への道 下』)181頁では、上記の道理を無視して
(4-2-13)
[ これは (4-2-12) 式の微分形 ］
等とやり、これを展開して、「固有時」や、「四元速度」、「四元加速度」、「相対論的運動量」、
「静止質量」、「Ｅ＝ｍｃ2」 、「一般相対論」等、馬鹿げた理論を続々と創り出しています。
間違いに間違いを重ねた理論の創出は、この後も延々続いているのですが、これより先は、
難しい式の羅列・展開となりまして、一般向け解説にはちょっと無理がありますので、やめます。
ただ、こういった誤った式の展開も全ては 
が 0 である事を
無視しようとする事から来るものです。
そして、もっと始末の悪い事には、この が相対論の一番最初
に出て来て、何にも予備知識の無い学生に誤った先入観を植え付けている事です。
教科書（ 『力学』 原島鮮著 裳華房 ） 291〜292頁では
「光速度不変の原理・・・・・・・・・・・・・・・・・・・・・
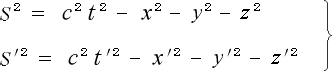(17.2 - 3)
とおこう。
，
は慣性系でどちらから見ても他方は一定の速度で動くから、 に対して一様な
直線運動は、 に対しても一様な直線運動でなければならない。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
光速度不変の原理により、
ならば 
でその逆も成り立つ。
従って 
と 
との関係は
(17.2‐4)
の形でなければならない。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
相対性原理によれば に対して成り立つ事は に対しても成り立たなければならないから
(17.2‐6)
でなければならない。(17.2‐4)，(17.2‐6)から
(17.2‐7)
つまり、k は・・・・定数で
＋１をとるか、−１をとるかである事がわかる。 v ＝０
の
場合を考えれば ＝ であるから k ＝１でなければならない。・・・」
等とやっています。
「何をやっているのか、良く解からない」と思われる方も多いでしょうが、少なくとも
「 と が必ずしも 0 とは限らない」
という前提で話を進めている事だけはお解かりになると思います。
と が 0 なら、この様な小難しい、いかにも厳密そうな論証は、最初から必要ありません。
実際 と は 0 なのですからこの様な論証は意味ありません。
しかしながら、これをやる事によって何も知らない学生達は、最初に
(4-2-14)
は 0 とは限らない、という先入観を与えられ、後に、四次元時空の所に来た時、
が 0 である事を無意識に否定し「これは四次元なのだ、三次元とは違う」などという
トンチンカンな事をやってしまいます。
実際、教科書や市販の本でも、この手の疑問を持ちそうな所では「これは三次元とは違うのだ」
と釘を刺し、それ以上疑問を差し挟まない様にしている物を多々見うけます。
そうなると、相対論の誤りは永久に正せません。「何か、おかしい？」と思っても、
「いや、自分が間違っているに違いない」と軌道修正してしまいます。
相対論の誤りは、低レベルの次元で見直さなければ判りません。
基本に立ち帰り、素人にも解かる様にと式をかみ砕いて見直した時、始めて判る事です。
相対論とは、実は、かくも、いい加減なものだったのです。
殆どが、アインシュタインの早とちりと勘違い、似た物との混同、或いは思い込みから
成り立っています。
高度な数学が使われている為、多くの人は、それに惑わされ、あたかも素晴らしい理論で
あるかの如く錯覚させられていますが、実は、とんでもない代物だったのです。
おまけにアインシュタインは、出来上がった式の意味を正しく理解していません。
間違って解釈していますから、そこから導かれる所の理論は、ことごとく、とんでもない
方向へと行ってしまいます。
相対論とは、言わば、ＳＦ映画の様な物です。映像の中では人は自由に空を飛べますし、
過去の世界へも行けます。
映像の中では、地上の物理法則や時間の順序を無視した何でもありの世界が創れるのです。
これと同じで、ちょっと似ているだけで無関係の式を用い、ルール無視でやれば何でも出来る
でしょう。
しかし、それは現実の世界とは関係ありません。ヴァーチャル・リアリティーの世界の話です。
相対論とは、実は、仮想現実の世界の話だったのです。
なお、私が言ってる事は“相対論の数式の解釈が間違っている”という事だけでして、別に
“相対論が予想しているような現象”まで存在しない、と断言しているわけではありません。
宇宙は広いですから、何があるか判りません。
もし、仮に、相対論の予想する様な現象が存在したとしても、
相対論が正しかったとは思わない方が良いでしょう。これは、間違っていますから。
その時はその時で、その現象を観測し分析して、そこから法則を見つけ出せばよいだけです。
それが科学という物でしょう。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る