四、四次元時空論の誤り
相対性理論では、この世界を三次元空間の他に時間を加えて四次元としています。
多くの人は、これについては「何か変だなー」とは思いながらも、偉い人が言うのだからそうかも
知れない、と思っておられるかも知れません。
ところで、相対論では、物の速度が光速を超える事は御法度となっています。
ところが、同じ相対論でも ブラックホール論では
「ブラックホールの入り口で物の落下速度は光速、
それより奥では光速を超えてしまい、光すらも外に出られない」とやっています。
これは矛盾する理屈です。
その為、相対論では「ブラックホールに入ると、時間と空間とが入れ替わってしまう」等と言う、
とんでもない理屈を創り出して、矛盾をごまかしました。これは滅茶苦茶な理屈です。
イメージして見て下さい。ロケットの進んでいる方向が突然時間に変わり、今まで時を刻んでいた
時間が空間に変わるという事を。イメージ出来ますか。無理でしょう。
時間がどうやって空間に変われるのです?
ここで、イメージしやすいように仮の話をしてみましょう。
進行方向の空間が突然、時間に変ったとします。
さて、そうすると、今まで、前方にあった星は何時に変るのでしょうか?
進行方向の空間が時間に変わると言いますが、左右上下方向の空間は元のままなのです。
なぜなら、左右上下方向は速度が 0 だからです。 速度 0 では時間と空間の交代はできません。
時間と空間が交代するには速度が光速を超える必要があるのです。
相対論の式でも、時間と入れ替わるのは  座標 つまり進行方向の空間だけとなっています。
座標 つまり進行方向の空間だけとなっています。
さて、そうすると、どういう事になるのでしょうか?
ロケットの左右上下の窓から見る景色は連続しています。
光速突破以前に斜め前に見えていた星は、光速突破後にも窓の外を横切ります。
時間に変った筈の空間 (星) が、左右上下から見ると元のままなのです。これをどうしますか?
そうすると、進行方向の空間と、左右上下方向の空間との整合性はどうなるのでしょうか?
このように、おかしな事になるのです。
相対論では、空間と時間とは入れ替え可能の物としています。
しかしながら、これは誤った式からつくられた理屈であって、正しくはありません。
そもそも、空間と時間とは全く異質の物で、同列に論じられるものではありません。
空間の次元は、縦・横・高さ 自由に移動出来ます。進む事も、戻る事も出来ます。
また、その場に留まる事も出来ます。それに対して、時間は戻る事も止まる事も出来ません。
只、一方的に前に流れるだけです。それも、こちらの自由にはなりません。
我々に自由度はないのです。我々が時間軸の中を進んでいるのではなく、
時間と言うベルトコンベアーの上に乗っかっている様な物ですから。
空間の次元と時間の次元とでは質が違います。
そういう事ですから空間の次元と時間の次元とを同列に扱う事は出来ません。
これは、それこそ別次元の話です。
そこで、ここでは、その誤りについて説明します。
まずは、この様な理論が、どの様にして出来たのかから説明して行きましょう。
(一)四次元時空の理論の誘導
(1)四次元座標の誘導
 (これは途中まではローレンツ変換の誘導と同じです)
(これは途中まではローレンツ変換の誘導と同じです)
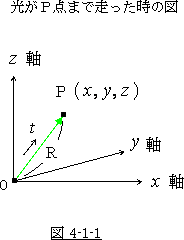
まずは、図 4-1-1 の様な直交座標を考えます。
そして、この座標系のある点 P( 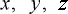 ) に原点 O より
) に原点 O より
光が走ったとしましょう。
そうすると、その距離は光速を 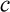 、走行時間を
、走行時間を  として
として
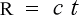 (4-1-1)
(4-1-1)
で求まります。次にピタゴラスの定理より、その距離の二乗は
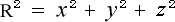 (4-1-2)
(4-1-2)
で求まります。この二式よりRを消去して
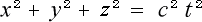 (4-1-3)
(4-1-3)
と置きましょう。そして次に、右辺を左辺に移項して
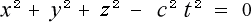 (4-1-4)
(4-1-4)
とおきます。ここまでは、ローレンツ変換の誘導と同じです。次からが違います。
この後、 (4-1-4)式を
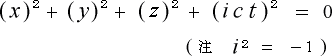 (4-1-5)
(4-1-5)
と言う風に書き換えるのです。
そうしておいて、座標の形態を今までの 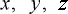 という方式から
という方式から 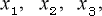 ・・・・ という
・・・・ という
形にやり換えます。
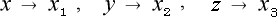
と言う様にです。それから (4-1-5) 式の4番目の項 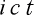 をも座標に組み入れて
をも座標に組み入れて 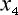 とします。
とします。
そうすると、新しい座標は
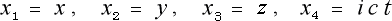 (4-1-6)
(4-1-6)
という形に置き換えられます。これが相対論の四次元座標です。
これを用いますと (4-1-5)式は
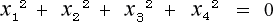 (4-1-7)
(4-1-7)
という形に置き換わります。
次に、座標の回転というものを考えましょう。
(2)座標の回転
教科書の原文はこちら
三次元空間では、原点 O から P 点までの距離をRとしますと 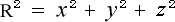 は座標の
は座標の
回転に対して、その値は変わりません。
いま Z軸 のまわりに θ だけ回転した座標系 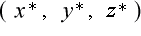 を考えます。
を考えます。
そうすると、同じP点の座標は新しい座標系では 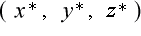 で表されます。
で表されます。
それを示したのが 図 4-1-2です。
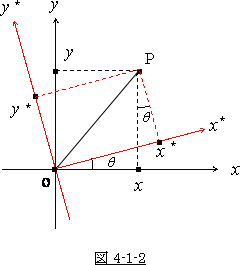 図より、前の座標と新しい座標との間には
図より、前の座標と新しい座標との間には
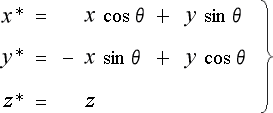 (4-1-8)
(4-1-8)
という関係が成立します。
これは、高等学校の数学の教科書に載っている事なので
証明はしません。
この場合、P点の座標は変わりますが、OP 間の距離は
変わりません。
(3)ローレンツ変換は四次元空間に於ける座標の回転の様な物
四次元座標
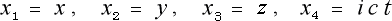
は既に求まっていますので、次はここに、ローレンツ変換 (2-1-8)
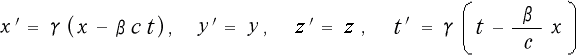 (2-1-8-1)
(2-1-8-1)
を持って来て、これに四次元座標を当てはめてみましょう。そうすると (2-1-8-1)は
( 途 中 計 算 省 略 )
(教科書も結果だけしか書いてない)
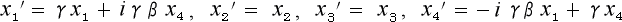 (4-1-9)
(4-1-9)
という形に置き換わります。
これが四次元座標を用いたローレンツ変換です。
ところで、ちょっと 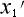 の項と
の項と 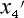 の項を比べてみて下さい。
の項を比べてみて下さい。
何か似ている事に気づかれませんか。
そこで、もっとはっきり判るように抜き出して並べて見ましょう。
そうすると
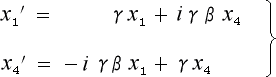 (4-1-10)
(4-1-10)
となりまして、何か、対照的な形である事が判かります。
実は、これは(4-1-8) の座標の回転の式に似ているのです。
ここで、仮に、 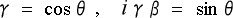 と置いて見ましょう。
と置いて見ましょう。
そうすると (4-1-10) 式は
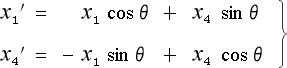 (4-1-11)
(4-1-11)
となりまして(4-1-8)の座標の回転の式
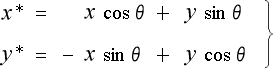 (4-1-8)
(4-1-8)
とそっくりになります。
そこから《ローレンツ変換は、四次元空間に於ける座標の回転の様な物だ》と見なされる様になった
のです。また、この事から《 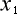 の座標と
の座標と 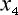 の座標とが、等価な物として交換可能》との解釈も
の座標とが、等価な物として交換可能》との解釈も
出て来ます。
ところで四番目の座標の 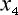 は
は 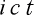 で実質的変数が時間の
で実質的変数が時間の  のみですから、四番目の座標軸を
のみですから、四番目の座標軸を
時間軸と見なせます。そしてまた 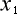 の座標は
の座標は  軸で、系の進行方向の座標です。
軸で、系の進行方向の座標です。
そこから、系の進行方向の空間次元と時間の次元とが同列に扱え、等価な物として交換可能という
解釈が出て来たわけです。
そして、ここより、四次元時空という概念が生まれ、ブラックホールに突入すると、時間と空間と
が入れ替わってしまう等という、とんでもない発想へと発展して行ったのです。
しかしながら、この理論は間違っています。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る
 (これは途中まではローレンツ変換の誘導と同じです)
(これは途中まではローレンツ変換の誘導と同じです)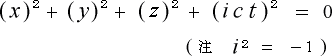

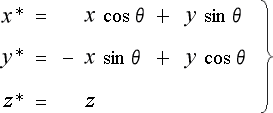 (4-1-8)
(4-1-8)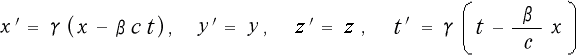
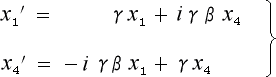 (4-1-10)
(4-1-10)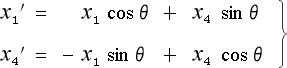 (4-1-11)
(4-1-11)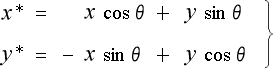 (4-1-8)
(4-1-8)