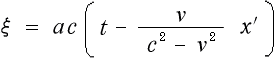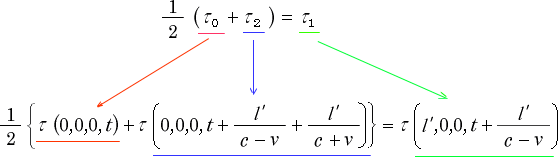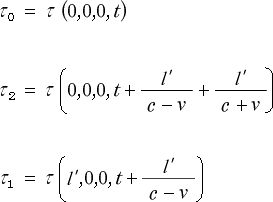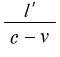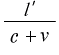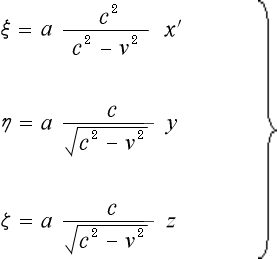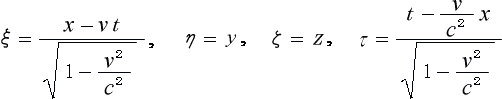(b) ローレンツ変換の誘導
次にアインシュタインは “光を往復させる思考実験” を “動く座標軸上”
に移して行い、
ローレンツ変換を誘導する事にしました。

この実験は、前項でも指摘しました通り間違って
いますので「ここより先の理論は全て誤っている」と
切って捨てる事も出来るのですが、他にも問題が有り
ますので、このまま行く事にします。
とは言いましても、ここの部分に関しましては非常
に高度な数学 (微分方程式) が使われていまして、一般
向けに解説するには、ちょっと困難なものがあります。
そこで、式の誘導過程全部を紹介するのは止めにして、おおざっぱに流しながら、問題のある所だけを
論評していく事にします。
ですから、難しい式が出てきても、無理に考えず流して下さい。
(イ) 座標と座標系の定義
原文はこちら
まず最初にアインシュタインは、座標系について定義をしました。
静止している系を静止系とし、これを K 系で表わし、
動いている座標系を運動系として、これを k 系で表わしました。
もっとも、これでは、どっちがとっちだか判らなくなりますので、ここでは、私の S系・ 系 に
系 に
統一する事にします。
次にアインシュタインは、各座標系の座標軸を図 3‐3‐2 の様に定めました。
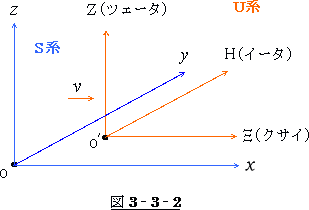
動いている系の  軸を Ξ(クサイ)軸に、
軸を Ξ(クサイ)軸に、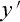 軸を Η(イータ)軸に、
軸を Η(イータ)軸に、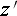 軸を Ζ(ツェータ)
軸を Ζ(ツェータ)
軸にしています。
注 Ξ はギリシャ文字で 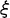 (クサイ)の大文字
(クサイ)の大文字
H はギリシャ文字で 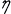 (イータ)の大文字
(イータ)の大文字
Ζ はギリシャ文字で 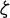 (ツェータ)の大文字
(ツェータ)の大文字
そして、その座標系に於ける、ある点の位置と時刻を座標形式で
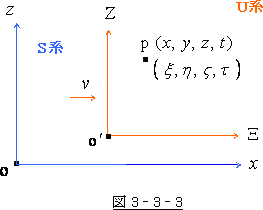 静止系については
静止系については 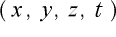 とし
とし
運動系については ( 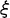 ,
, 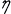 ,
, 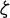 ,
, 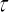 ) と
) と
しました。
その上で、彼は、
《これら二組の数値を結び付ける関係式を発見する
のが、ここの課題だ》
と言っています。
確かに、その通りに行けば、出来上がった関係式(ローレンツ変換)は、座標と時刻の関係式に
なっている筈です。 実際には 距離と時間の関係式になっているのですけど。
だから勘違いをしたわけです。この後、彼は
《 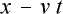 を
を  と書く事にすれば、
と書く事にすれば、 系 に静止している任意の点 (
系 に静止している任意の点 ( 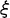 ,
, 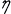 ,
, 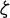 ) は
) は
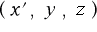 という3個の数値の組によって位置が規定される。》
という3個の数値の組によって位置が規定される。》
としました。
何を言いたいのかと言うと、要するに、 系 の座標をS系 の数値でもって表わしたい
系 の座標をS系 の数値でもって表わしたい
という事のようです。
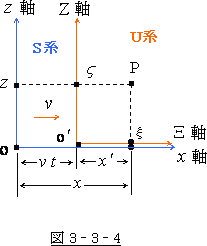
動いているのは、 軸方向だけですから
軸方向だけですから 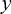 軸方向・
軸方向・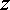 軸方向
軸方向
の座標に変化はありません。
従って、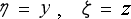 と置き換えても差し支えなくなります。
と置き換えても差し支えなくなります。
問題は  軸方向だけです。
軸方向だけです。
この方向は動いていますので関係式が必要となります。
それは 図 3‐3‐4 より与えられます。
この図より、
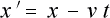
が成り立ちますので、これを使おうというわけです。
ここで  系のΞ 座標の
系のΞ 座標の 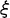 に相当する部分を距離
に相当する部分を距離  でもって代用すれば、
でもって代用すれば、
《  系の任意の点の座標 (
系の任意の点の座標 ( 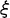 ,
, 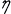 ,
, 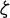 ) は
) は 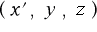 という3個の数値に置き換えられる》
という3個の数値に置き換えられる》
と言ってるわけです。
そして  は
は 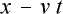 ですから、これは事実上“
ですから、これは事実上“  系 の数値を S系 の数値でもって表わし
系 の数値を S系 の数値でもって表わし
た”事になります。
こうしておいてアインシュタインは、《動く座標軸上で光を往復させる思考実験》に移りました。

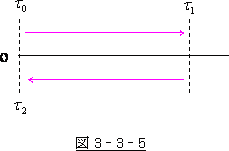 系 の時刻で
系 の時刻で 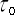 の時に、
の時に、 系 の原点 Oより光が
系 の原点 Oより光が  軸
軸
方向に向けて発され、固定点で時刻 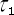 に反射されて、時刻
に反射されて、時刻
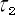 に戻ったとする。 そうすると
に戻ったとする。 そうすると  系 では
系 では
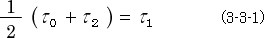
が成り立つ。
これを静止系で見、独立変数 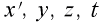 を用いて、
を用いて、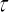 を
を 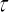 (
(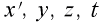 ) の形で
) の形で
書けば上式は
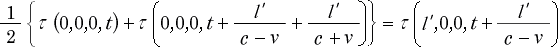 (3-3-2)
(3-3-2)
となるが、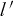 を無限少量とすればこの関係式は
を無限少量とすればこの関係式は
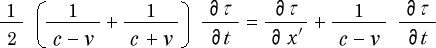 (3-3-3)
(3-3-3)
という微分方程式で表わせる。そして、これは
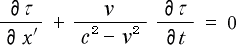 (3-3-4)
(3-3-4)
とも書き換えられる。
とやっています。この辺は難しいので解説はしません。
続けてアインシュタインは、
今まで述べた議論と同じ事を Η軸 及び Ζ軸 方向に適用すれば 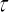 に関して
に関して
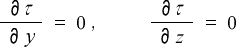 (3-3-5)
(3-3-5)
が得られる。この式を導くに当たり注意すべき点は、S系 から眺めた時 Η 或いは Ζ 軸方向
への光の伝播速度が 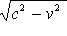 であるという事である。
であるという事である。
と言っています。
難しい所は無視して下線部分 (光の伝播速度が 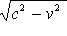 である) に着目して下さい。
である) に着目して下さい。
これは彼の言う「光速度不変の原理」に反しないのでしょうか。
それが通るのなら、動いている物体より発された光の速度は、それを静止系より見た場合 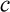 でなくても
でなくても
良い事になります。
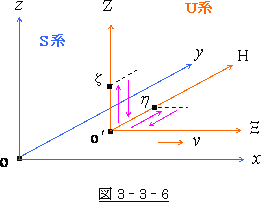
と言っても「何の事か良く解からない」と思われる方も
多いでしょうから説明します。
前の話は、Ξ(クサイ)軸(つまり  軸)方向に光を
軸)方向に光を
走らせての話でしたが、今度は Η(イータ)軸(つまり 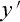
軸)及び Ζ(ツェータ)軸 方向に光を走らせての話です。
これは  系 の Η軸 または Ζ軸 方向に光を走らせた場合、
系 の Η軸 または Ζ軸 方向に光を走らせた場合、
それを S系 から見るとどう見えるかという話です。
両方書くと、判りづらいので Ζ軸 方向だけで話を進めてみましょう。
時刻 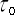 に光が発され、時刻
に光が発され、時刻 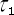 にΖ軸の座標
にΖ軸の座標 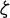 の所で反射されて、時刻
の所で反射されて、時刻 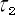 に光が原点O′に戻って
に光が原点O′に戻って
来たとします。
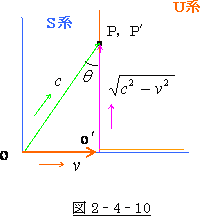
これを  系 で見れば図 3‐3‐7の様になりますが、S系 から見れば図 3‐3‐8 の様になります。
系 で見れば図 3‐3‐7の様になりますが、S系 から見れば図 3‐3‐8 の様になります。
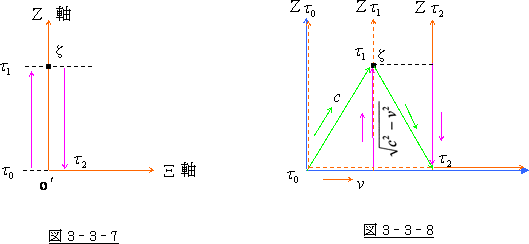
U系 は動いていますので、S系 より見た所の各時刻での光の位置は図 3‐3‐8の様になり、
その軌跡は三角形になります。
この状態で、S系 より見た所の光速を 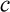 としたなら、
としたなら、 系 に於ける光速は三角関数により
系 に於ける光速は三角関数により
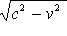 になるということです。
になるということです。
しかし、こういう事をする位なら、 系 での光速を
系 での光速を 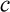 のままにしておいて、S系 より見た所の
のままにしておいて、S系 より見た所の
光速を 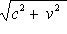 にした方が、よほど解かりやすいのでは、と思うのですが、アインシュタインは、
にした方が、よほど解かりやすいのでは、と思うのですが、アインシュタインは、
そうはしません。
彼は、光速 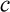 を絶対とし、これを超える速度は無いとしていますので、S系 より見た所の光速を
を絶対とし、これを超える速度は無いとしていますので、S系 より見た所の光速を 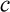
より大きく出来ないのです。
しかし、それなら、S系 より見た所のΖ軸方向の光速を 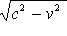 とするのも変でしょう。
とするのも変でしょう。
これでは光速は 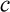 より小さくなってしまいます。これは光速度不変の原理に反しないのでしょうか。
より小さくなってしまいます。これは光速度不変の原理に反しないのでしょうか。
何ともウサン臭い気がします。
こういう所は、どうも恣意(しい)的というか、いい加減に行われている様です。
それは、ともかく、これは私が、前章の第三節「時間の遅れ」の
所で《  系内で原点 O′より
系内で原点 O′より  軸に垂直に光を発し、それをS系
軸に垂直に光を発し、それをS系
より観測した場合の光速を 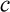 とすれば、
とすれば、 系内での光速は三角関数に
系内での光速は三角関数に
より、便宜上 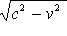 になる》としたのと同じ事でしょう。
になる》としたのと同じ事でしょう。
私は「動いている系での光速」と「それを静止系から見た場合
の光速」とは違うという前提でやっていたのですが、同じ事をアイ
ンシュタインですらやっていたのなら、私が非難される筋合いは
ないと思われます。
またアインシュタインは、別の所では《一方、S(K)系から見れば、 (k)系の原点に対する光の
(k)系の原点に対する光の
先端の相対速度は 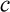 −
− 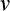 である》ともしています。
である》ともしています。
彼は、一方では光速は絶対不変としながら、他方ではこの様に好き勝手に変化させているのです。
かなりの御都合主義でしょう。
その次にアインシュタインは《以上三個の方程式から
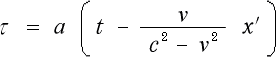 (3-3-6)
(3-3-6)
が導かれる》としています。多分、微分方程式を解けばこうなる という事でしょう
この後《 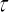 =0の瞬間に、
=0の瞬間に、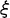 の増加する方向に向けて光が
の増加する方向に向けて光が  系の原点から発射されたとしよう。
系の原点から発射されたとしよう。
この光に対しては
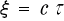 (3-3-7)
(3-3-7)
が成立する》としています。
しかし、これも問題です。
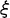 は確か、
は確か、 系 の任意の点のΞ 座標だった筈です。(
系 の任意の点のΞ 座標だった筈です。( 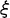 ,
, 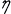 ,
, 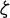 ,
, 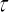 )でしたから。
)でしたから。
それに対して 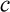
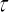 は光の走行距離です。
は光の走行距離です。
こんな事をすると 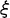 は光の走行距離になってしまいます。
は光の走行距離になってしまいます。
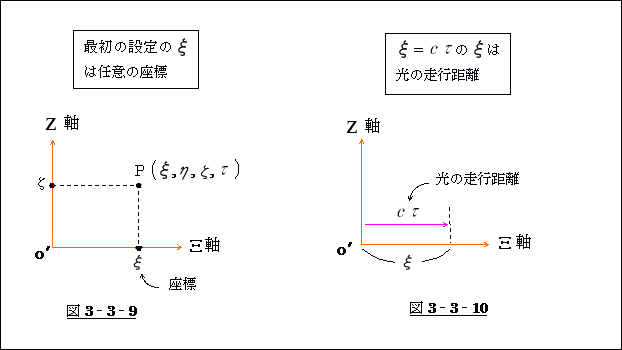
座標と見なしても、光が 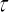 時間掛けて到達した所のΞ 軸上の位置にしかなりません。
時間掛けて到達した所のΞ 軸上の位置にしかなりません。
これより後の 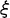 は、任意の座標ではなくなってしまうのです。
は、任意の座標ではなくなってしまうのです。
次に 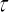 ですが、これも光の走行時間です。もっとも《
ですが、これも光の走行時間です。もっとも《 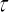 =0の瞬間に光が発射され》とありました
=0の瞬間に光が発射され》とありました
ので、これを光の到達時刻と見なす事は出来ます。がしかし、任意の時刻とまでは見なせません。
はっきり言える事は 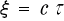 は光の走行距離と走行時間の関係式だという事です。
は光の走行距離と走行時間の関係式だという事です。
これを光の到達位置と到達時刻の関係式と見なす事は出来ますが、その代わり 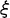 と
と 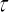 は、
は、
任意の座標や任意の時刻ではなくなってしまいます。
これ以後の 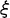 と
と 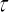 は《光が走った所の距離と時間》または《到達位置と到達時刻》になってしまうの
は《光が走った所の距離と時間》または《到達位置と到達時刻》になってしまうの
です。
次にアインシュタインは、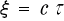 に(3-3-6) 式を代入して
に(3-3-6) 式を代入して
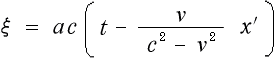 (3-3-8)
(3-3-8)
としました。
そして複雑な計算をした後でローレンツ変換を導き出しています。
ここでのローレンツ変換の誘導は、ちょっと見には、私が学校で習ったやり方と全く違っている
様に見えたのですが、本質的には同じ事だったのです。
《光の走った距離と時間》とから関係式を導き出していますから。
この式の誘導過程では、一見、勘違いを招く様なやり方がしてあります。
例えば、この節の最初の光の往復の所に
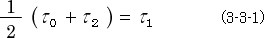

と言うのがありました。
ここでは 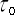 も
も 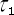 も
も 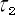 も時刻です。従ってこの式は誰が見ても時刻の式です。
も時刻です。従ってこの式は誰が見ても時刻の式です。
ところがこの式は、本当は時間の式と言うべき物なのです。
なぜなら後で、微分方程式にしているからです。 この式は次に
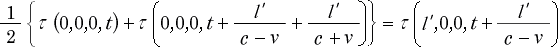
とややこしく展開されています。
(3-3-1) 式が何で、こうなるのかについては、私は説明出来ません。
ただ高等数学では良く使われる手法だという事だけは言えます。
この式の細部は次の様になっています。
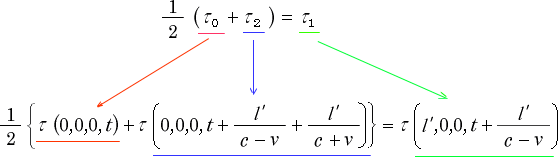
具体的には
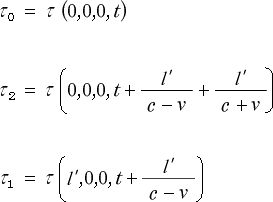
です。 ここで 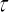 ( 0,0,0,t ) を分解しますと
( 0,0,0,t ) を分解しますと

となります。従ってここの  は誰が見ても時刻です。ところが次の
は誰が見ても時刻です。ところが次の 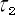 の所では
の所では
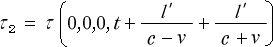
となっていて、時刻の所に 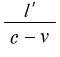 や
や 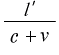 が入っています。この
が入っています。この 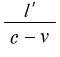 は、前節の
は、前節の
「時刻の相対性」の所で出て来た様に《光の往きの走行時間》です。そして 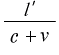 は《光の還りの
は《光の還りの
走行時間》です。もちろん 時刻 + 時間 = 時刻 になりますけど。では、次はどうでしょう。
その次に 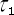 では
では
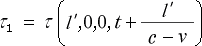
となっていて、 座標の所に距離の 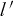 が堂々と入っています。
が堂々と入っています。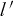 は《光の走行距離》です。ここでは
は《光の走行距離》です。ここでは
《座標》の位置に《光の走行距離》が堂々と入っていたり、《時刻》の位置に《光の走行時間》が入って
いたりしているのです。
その次にアインシュタインは、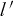 を無限小量とすれば、この関係式は
を無限小量とすれば、この関係式は
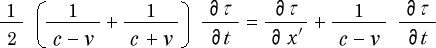
という微分方程式になる としました。
これも何故(3-3-2) 式からこうなるのか説明できません。かつ、あの様に象徴的に書いただけの
座標形式の式を、そのまま微分方程式にして良いのかどうかも、良く解かりません。
ただ、無限小量という言葉自体長さを持っている事の証拠だと言う事は出来ます。
時間にしろ距離にしろ、長さを持っているから微分出来るのです。長さを持たない「時刻」や
「座標」では微分出来ません。
そう言うと「実際の物理では、時刻や座標を微分しているではないか」と言われそうですが、
それは勘違いという物です。その「時刻」や「座標」の近傍には0と見なしても良い程の微小な
幅が有るとして微分しているのです。従って本当は「時刻」や「座標」で微分しているのではなく、
「時間」や「距離」で微分しているのです。
微分方程式の前までは時刻や座標の関係式と見なしても構いませんが、微分方程式より後では、
光の走行時間と走行距離の関係式になってしまいます。
従って、これを解いて出て来た式
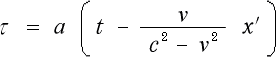
は、当然、光の走行距離と走行時間の関係式ということになります。
その上、 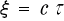 も光の走行距離と時間の関係式ですから、これを (3-3-6)式 に代入して
も光の走行距離と時間の関係式ですから、これを (3-3-6)式 に代入して
出来た式 (3-3-8)
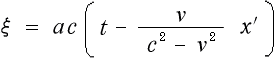
もまた、当然の事ながら、光の走行距離と時間の関係式ということになります。
この後、ややこしい計算をして
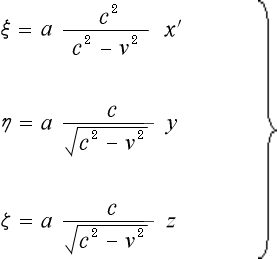 (3-3-9)
(3-3-9)
を出し、段々とローレンツ変換に近づけて行き、最終的に
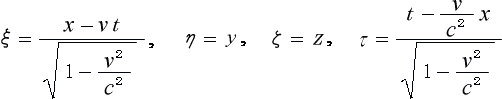 (3-3-10)
(3-3-10)
(式は途中省略しています。詳しくは原分を見て下さい)
という形(ローレンツ変換)に仕上げて行きますが、 これらの過程を見て行きますと、難解な所
やウサン臭い所は無視しても、ローレンツ変換が光の走行距離と走行時間の関係式である事は明白
となります。
従って、ローレンツ変換は光の走行距離と走行時間の関係式なのです。
これは、任意の座標や任意の時刻を求める式等ではありません。
その基本に立ち返れば、私が学校で習ったローレンツ変換の求め方も基本的に同じだった事が
判ってきます。
アインシュタインは、Ξ軸、H軸、Ζ軸 バラバラに光を走らせましたが、教科書は最初から
斜めに光を走らせて
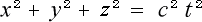
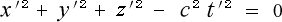
としました。そこで、三方向は同時に計算出来ます。
そしてアインシュタインは、ここでは紹介しませんでしたが、球面波として
静止系 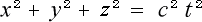
運動系 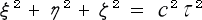
という式を挙げています。これを連立方程式に用いれば、一挙にローレンツ変換が作れます。
私が学校で習ったやり方は、一見、アインシュタインのやり方と違っている様に見えたのですが、
本質的には同じ事だったのです。
ただ、アインシュタインの時より、スマートで、合理的で、簡単なやり方に進化していただけです。
アインシュタインのやり方は、杜撰な所が多くて解かりにくいので、多くの先生方が寄ってたかっ
て改良し、今のような形に仕上げ直していったのでしょう。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る


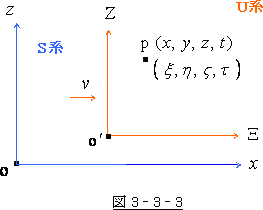





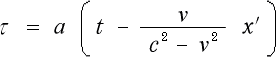 (3-3-6)
(3-3-6)