ローレンツ変換に四次元座標を組み込んで出来た式
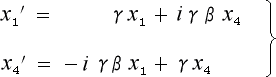(4-1-10)の γ を cosθ に iγβ を sinθ に置き換えてみたら
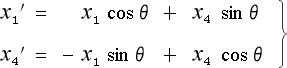(4-1-11)となって、座標の回転の式とそっくりになった。「だから、ローレンツ変換は四次元空間に於ける
座標の回転の様な物だ。」という事ですが、果たして、そうなのでしょうか。
ローレンツ変換に四次元座標を組み込んで出来た式
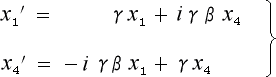(4-1-10)
の γ を cosθ に iγβ を sinθ に置き換えてみたら
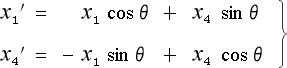(4-1-11)
となって、座標の回転の式とそっくりになった。「だから、ローレンツ変換は四次元空間に於ける
座標の回転の様な物だ。」という事ですが、果たして、そうなのでしょうか。
仮に置いた γ ＝ cosθ, iγβ ＝ sinθ に問題は無いのでしょうか。
実は、あるのです。
γ ＝ cosθ は、まあよいとしましょう。しかし iγβ ＝ sinθ には問題があります。
iγβ の中には γ が入っているのです。
という事は sinθ の中には cosθ が入っているという事になります。 それは
sinθ ＝ iγβ ＝ iβcosθ (4-2-1)
という事で sinθ は cosθ に比例するという事になるの
ですが、それでも良いのでしょうか。
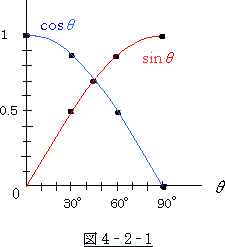
そもそも sinθ と cosθ とは逆の関係にあります。
cosθ が大きくなれば sinθ は小さくなり、
cosθ が小さくなれば sinθ は大きくなります。
cosθ ＝ 1 のとき sinθ＝ 0
cosθ ＝ 0 のとき sinθ＝ 1
です。
どうして、 sinθ が cosθ に比例出来るのでしょうか。
このこじつけには無理があります。それだけではありません。
この三角関数の間違いには、まだ奥があるのです。
そこで、この三角関数の問題について、もっと詳しく調べてみましょう。
まずは、 γ ＝ cosθ からです。
γ の元の式は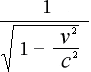 
でした。これを整理して単純化してみましょう。
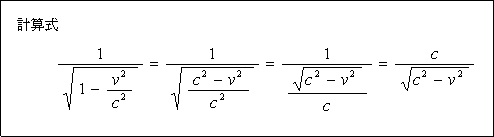
そうすると 
になります。
従って、cosθ ＝ です。
ところで、この式をよく見て下さい。分子より分母の方が小さいのです。
分子より分母の小さい cosθ があるでしょうか。
これでは cosθ＞１ になってしまいます。
本来 cosθ は 0 ≦｜cosθ｜≦ 1 なのです。
次に sinθ の式も同様に単純化してみましょう。
そうすると sin θ ＝ 
になります。
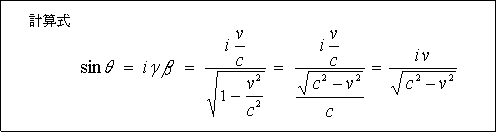
単純化された cosθ と sinθ が求まりましたので、これを並べてみます。
cosθ ＝ , sin θ ＝ (4-2-2)
そして、これを元にして三角形を描いてみましょう。
そうすると、それは、図4‐2‐2の様になります。
図をよく見てください。何か変ではありませんか。
斜辺（イーハ）の寸法 
の方が辺（イーロ）の寸法 c
より短いのです。これは論理的に矛盾します。
直角三角形では、斜辺は他の二辺より長くなければなりません。
これでは直角三角形は成り立ちません。
（注 ： 虚数の記号 i は実数と方向が 90°違う事を差し示すだけなの
で、無視して数値のみで扱っております。)
もっとも、辺（イーハ）の寸法と辺（イーロ）の寸法とを入れ
替えれば、直角三角形は成り立ちます。
が、しかしそれでは、相対論が望む方向への理論誘導はできません。
従って、この三角関数のこじつけは全くの誤りとなります。
こんな物をこじつけられて、「座標の回転の式とそっくりになった」と言われても、
苦笑せざるを得ません。
直角三角形の成り立たない三角関数では、座標の回転に適用のしようがありませんから。
座標の回転の角度 θ は直角三角形の角度 θ なのです。
本を書かれている人の中には、これを指摘されるのを警戒されてか、 cosθ、 sinθ とせず、
ハイパー cosθ、ハイパー sinθ とされておられる方がいます。しかし、どうごまかそうとも、
座標の回転は直角三角形で成り立つ話ですから、直角三角形の理屈が成り立たなければ、この理論も
成り立ちようがありません。
従って、教科書の言う“ローレンツ変換は四次元空間に於ける座標の回転の様な物だ”
という“考え”は全くの誤りとなります。
同じこじつけるにしても、もう少し、つじつまを合わせてからこじつけて欲しい物です。
三角関数がでたらめなのですから、座標の回転も時空の転換もありません。
四次元時空などまったくの絵空事となります。
ところで、図4‐2‐2を良く見て下さい。この図は、動いている系の速度と光速との関係を
表している様にも、見えませんか？
実は、この三角関数は、そこにこそ本当の意味が有ったのです。
座標の回転などではありません。 次は、その説明です。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る