�i��j�@��Ԃ̒��̎��Ԃ̖���
�i���j�����Ă����Ԃ̒��ł͎��Ԃ��x���i����j
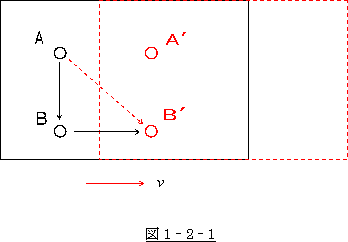
�@�E�}�́A��Ԃ̒��̗l�q�����������ł��B
�@ �`�C�a�͍��Ȃ̈ʒu�ł��B��Ԃ͑��x
�E�����ɓ����Ă��镨�Ƃ��܂��B
�@�����ŁA�`�̍��Ȃ̐l���������z���ׂɁA
���C�^�[�ʼn�_�����Ƃ��܂��傤�B
�@��������ƁA���̌��͂a�̐l�ɂ́A�܂�����
�`���a�̕����֗����l�Ɍ����܂��B
�@�Ƃ��낪�A������O���猩�Ă����l�ɂ́A
���͂`���a���̕����֗����l�Ɍ����܂��B
�@���������瑬���Ƃ͌����A�`����a�ɓ͂��Ԃɗ�Ԃ������͑O�ɓ����Ă��邩��ł��B
�@��������ƁA��Ԃ̊O���猩�����̑��s�����́A��Ԃ̒��Ō������̑��s�������������Ȃ�܂��B
�@����́A���Θ_�ȑO�̍l�����ł����Ȃ�A
�@�u��Ԃ������Ă���̂����瓖����O�ł͂Ȃ����A��Ԃ̊O���猩�����̑��x�́A��Ԃ̒���
�������̑��x����Ԃ̑��x�����Z����Ă���B�����炻�̕��A�������L�тē��R�v
�ƂȂ�̂ł����A���Θ_�ł́A
�@�@�@�@�@�@�s���̑��x����Ԃ̒����猩�Ă��A�O���猩�Ă������t
�ƂȂ��Ă��܂��̂ŁA�����͍s���܂���B
�@���Θ_�ł́A�]��������O�����������A������O�ł͒ʂ�Ȃ��̂ł��B
�@�ł́A�ǂ�������悢�̂ł��傤���B
�@���̏ꍇ�ɂ́A���Ԃ̕���ς���̂ł��B
�@�܂��́A���x�̎���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@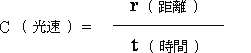 �@ �@�@�@�@�@�@�@�@�@�@�@�@�@(1�]2�]1)
�@ �@�@�@�@�@�@�@�@�@�@�@�@�@(1�]2�]1)
�Ƃ��āA�����Ǝ��Ԃ̊W�����Ă݂܂��傤�B
�@�@�@�@�@�@�@�@��ԓ��Ō������̑��s���Ԃ��@�@�@�@�@�@�@t
�@�@�@�@�@�@�@�@��ԊO���猩�����̑��s���Ԃ��@�@�@�@�@�@t��
�@�@�@�@�@�@�@�@��ԓ��Ō������̑��s�������@�@�@�@�@�@�@�`�a
�@�@�@�@�@�@�@�@��ԊO���猩�����̑��s�������@�@�@�@�@�@�`�a��
�Ƃ����
�@�@�@�@�@�@�@�@�@�@�@��ԓ��ł̌��̑��x���@�@�@�@�@�@�@�@�@�@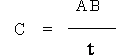 �@�@�@�@�@�@�@ �@�@(1�]2�]2)
�@�@�@�@�@�@�@ �@�@(1�]2�]2)
�@�@�@�@�@�@�@�@�@�@�@��ԊO���猩�����̑��x�� �@�@�@�@�@�@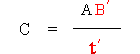 �@�@�@�@�@�@�@ �@�@(1�]2�]3)
�@�@�@�@�@�@�@ �@�@(1�]2�]3)
�ƂȂ�܂��B�����ŁA���̓�̎������킹�܂���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@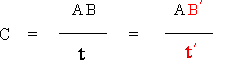 �@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@(1-2-4)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@(1-2-4)
�ƂȂ�܂����A�}1-2-1 �ł�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�`�a�@���@�`�a���@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@�@(1-2-5)
�ł�����A����� (1-2-4) ���ɓ��Ă͂߂Ă݂܂���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ t�@���@t���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (1-2-6)
�ƂȂ�܂��B�@���̌��ʂ�
�s�������̓`��錻�ۂł��A��ԓ��ł̕����A�O���猩��������̓`�d���Ԃ��Z���t
�Ƃ�������\�킵�Ă��܂��B
�@����́A��Ԃ̒��̕����O�������v�̐i�ݕ������Ȃ��A�Ƃ�������
�s�����Ă����Ԃ̒��ł��A�O�ɔ�ׂ����Ԃ��x����t�Ƃ������ɂȂ�킯�ł��B
�@���ꂪ�A���Θ_�ŗǂ������鏊��
�@�@�@�@�@�@�@�u�����Ă���n�ł��Î~�n�������Ԃ��x����v
���������_�̂₳���������̈�ł��B�����܂ł͒���ʂ�ł��B
�@�@�@�@(�� �F ����͎��Ǝ��̍l���ł͂Ȃ��A�w���㕨���̐��E�]�T ���ΐ����_�Ɨʎq�͊w�̒a���x
�@�@�@�@�@�@ �u�k�������ɂ����掵�́u���v�̃p���h�b�N�X�v�̂�����^�������̂ł��B�j
�@���Ď����炪���ł��B
�ib�j�@�����Ă����Ԃ̒��ł͎��Ԃ��i�ށH
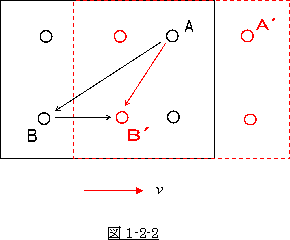 �E�̐}1�]�Q�]�Q����������B
�E�̐}1�]�Q�]�Q����������B�@�������ԓ��̗l�q�ł����A�`�Ƃa�̐l�͑Ίp�����
�����������č����Ă��܂��B
�@���A�����ŁA�`�̍��Ȃ̐l���������z���ׂɁA���C�^�[
�ʼn�_�����Ƃ��܂��傤�B��������ƁA���̌��͂a��
�l�ɂ́A�܂������`���a�̕����֗����l�Ɍ����܂��B
�@ �Ƃ��낪�A���̌��i���O���猩�Ă����l�ɂ́A����
�`���a���̕����֗����l�Ɍ����܂��B
�@���������瑬���Ƃ͌����A�`����a�ɓ͂��Ԃɗ�Ԃ������͑O�ɓ����Ă��邩��ł��B
�@�}1�]2�]2 �ł͂`�a�����`�a���̕����������Z���̂ŁA��Ԃ̊O���猩�����̑��s�����̕����A
��Ԃ̒��Ō������̑��s���������Z���Ȃ�܂��B
�@����͑O�Ɣ��̌��ʂł��B
�@�O�Ɠ��l�ɂ��ċ����Ǝ��Ԃ̊W�����߂Ă݂܂���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
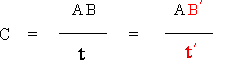 �@�@�@�@�@�@�@�@�@�@�@(1�]2�]7)
�@�@�@�@�@�@�@�@�@�@�@(1�]2�]7)�ƂȂ�܂��B�@�}1�]2�]2 �ł�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�`�a�@���@�`�a���@�@�@�@�@�@�@�@�@�@(1-2-8)
�ł�����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ t�@���@t�� �@�@�@�@�@�@�@�@�@�@ (1-2-9)
�ƂȂ�܂��B
�@��������ƁA���x�����̑��s���Ԃ́A��Ԃ̒��̕����O�����]�����|�������ɂȂ�܂����B
�@����́A����������A��Ԃ̒��̕����O�������v�������i�ށA�܂����Ԃ��i���Ƃ������ɂȂ�킯�ł��B
�@�O�Ɠ��������ł�����̂ɁA���x�́A��Ԃ̒��̕����O�������Ԃ��i�ގ��ɂȂ�܂����B
�@�}1�]2�]�P �̏�Ԃł́A��ԓ��̎��Ԃ��O���x�ꂽ�̂ł����A
�@�}1�]2�]2 �̏�Ԃł��t�ɐi�ގ��ɂȂ�̂ł��B
�@����͈�̂ǂ��������ł��傤���B
�@������ԓ��ł̌��̎����Ȃ̂ɁA�������錋�ʂ��o�ė��܂����B
�@���̓�̏�Ԃ͈�̂ǂ����Ⴄ�̂ł��傤���B
�@����́A���́A���̐i�ޕ����Ȃ̂ł��B
�@�����ŁA���̕������A����������ʉ����Ē��ׂČ��܂��傤
(��)�@���̐i�ޕ����ɂ���Ď��Ԃ̒x��i����قȂ�H
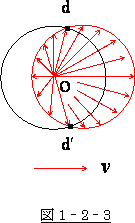
�@�}1�]�Q�]�R�����ĉ������B
�@�~����`���Ă���A�E���̉~�ɂ�������`���Ă���܂��B
�@�܂��A�����̉~�ł����A����́A��ԓ��̈�_�O���������A���
�̎��Ԃɓ��B����ʒu�i��ԓ����猩���j�ł��B
�@�����āA�E���̉~�́A���̈ʒu����Ԃ̊O���猩���ꍇ�̈ʒu�ł��B
�@��Ԃ͓����Ă��܂��̂ŁA�~�͉E���Ɉړ����܂��B
�]���āA�����̉~�̒��S�O�������́A�E���̉~�ɓ��B���鎖�ɂȂ�܂��B
�@��Ԃ̒��ł��A���͈��̎��ԂɈ��̋�����i�ނ̂ł����A������O���猩�Ă���ƁA���̋���
�́A�i�ޕ����ɂ���ă}�`�}�`�ɂȂ�܂��B�@����ɑ��Θ_�̗����Ă͂߁A�����ɉ��߂��悤��
����A���Ԃ̒x��i��݂͂ȈقȂ��ė��܂��B
�@�O�̂����ł́A�O���猩�����̌��̋����̒��������A��ԓ��̎��Ԃ��x��Ă��܂����̂ŁA������
���p���܂��ƁA�~�̔��a������������ �i��{�I�ɑO���ɔ��ˁj �����Ԃ��x���A�Z���� �i��{�I�Ɍ��
�ɔ��ˁj �����Ԃ��i�����ɂȂ�܂��B
�@������ӏ����������Ƃ����������̂ݎ��Ԃ͒x����i�݂����܂��B
�@���̑��̕����ł́A���̒������F�Ⴂ�܂��̂ŁA���Ԃ̒x��i��͑S���قȂ��ė��܂��B
�@�����������甭�������Ȃ̂ɁA�ǂ̕����Ɍ�����������ɍ̂邩�ŁA�����̎��Ԃ̐i�ݒx�ꂮ����
���قȂ��ė���̂ł��B
�@�S���n���������ł����A���́A�S�̂͂����Ȃ��Ă����̂ł��B
�@���Θ_�ŁA�悭�g���鏊�̗�́A���̖����ɂ�����̕����̂ق�̈�������̂����ɉ߂��܂���B
�i���j�@���Ԃ͒x������Ȃ���ΐi�݂����Ȃ�
�@���ɑ��������痈����ōl���Ă݂܂��傤�B
�@���܂ł̂́A�P������ł̘b�ł������A���ۂ̏ꍇ�A�����͑�R����܂��B
�@���͑O�������납��������ɗ��܂��B���������ꍇ�ǂ��Ȃ�̂ł��傤���B
�@�Î~���Ă��鎞�́A�Ƃ������A�����Ă����Ԃɏ���Ă���ꍇ�A�i�s�����ɑ����O���痈���
����ɂ��āg�����x�s�ς̌����h�ōl��������Ԃ͐i���A��납�痈����ōl��������Ԃ͒x���
���ɂȂ�܂��B
�@����́A�S���A�Œ��ꒃ�Șb�ł�
�@�����A�ǂ������痈�悤�ƁA���̏u�Ԃ̂��̏ꏊ�̎��Ԃ͓����ł��傤�B
�@���������ꍇ�A�s���Ԃ͒x������Ȃ���ΐi�݂����Ȃ��t�ƍl����̂��Ó�(���Ƃ�)�ł��B
�@�����ŁA���Θ_�ɏڂ������́A�u�A�C���V���^�C���́w���Ԃ��x���x�Ƃ͌��������A�w�i�ށx�Ƃ�
�����Ă��Ȃ��A������A���O�̗����͐��藧���Ȃ��v�Ƃ�������邩���m��܂���B
�@�Ƃ��낪�A���ׂĂ����ƁA���̖������o�Ă���̂ł��B
�@����́A���������A�Љ�Ă����܂��B
�@���̑O�ɁA�ȒP�ȏ����瓖�����Ă����܂��傤�B
�@�܂��A���̔n���������ʂɂȂ�����������ł��B
�@�Ȃ��A�����Ȃ����̂��H
�@����́A�A�C���V���^�C�����s���̑��x�͐���t�Ƃ�������ł��B
�@�s�����Ă���n���猩�Ă��A�Î~���Ă���n���猩�Ă������͓����t
�Ƃ��Ă��܂�������A�������������������Ă��܂����̂ł��B
�@���͂����ɂ���܂��B
�@���́A����ɂ��Ăł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�����@�@�@�@�@�@ �@�@�ł̓��ɖ߂��@�@�@�@�@�@�@�@�O�̕łɖ߂��@�@�@�@�@�@�@�@ HOME�ɖ߂�