それには、まず U 系 の原点 O′より
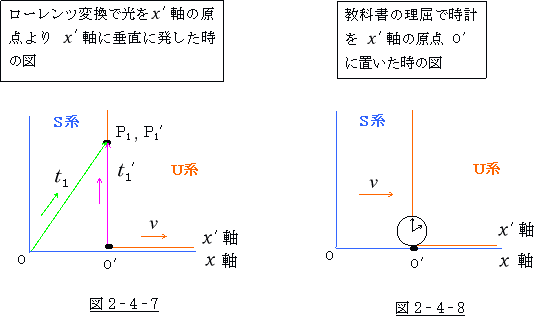
そうすると、その図は 図2‐4‐7 の様になります。
(c) 式の意味する所
それには、まず U 系 の原点 O′より ![]() 軸に垂直に光を発し、それを S系から観測する事です。
軸に垂直に光を発し、それを S系から観測する事です。
そうすると、その図は 図2‐4‐7 の様になります。

この場合、光の到達点の ![]() 座標 は、いかなる時でも O′ですから一定となり、教科書の設定と
座標 は、いかなる時でも O′ですから一定となり、教科書の設定と
合致する事になります。
つまりこういう場合でなら ![]() を時計の位置と見なしても差し支えなくなるのです。
を時計の位置と見なしても差し支えなくなるのです。
そしてこういう状態でなら“時間の遅れ論”の元となった 式 (2-4-3)
![]() (2-4-3)
(2-4-3)
は成り立ちます。そこで、次は、この式の意味について考えて見ましょう。
まずは 図 2‐4‐9 に着目して下さい。
光の発される時を0時、![]() 1 を1時、
1 を1時、![]() 2 を2時とすれば
2 を2時とすれば
![]() −
− ![]() の長さは
の長さは ![]() −0 と同じになり
−0 と同じになり
![]() 2 −
2 − ![]() 1 の長さは
1 の長さは ![]() 1 −0 と同じになります。
1 −0 と同じになります。
ということは (2‐4‐3) の式は
![]() (2-4-4)
(2-4-4)
で置き換えても同じという事です。
これは 図 2‐4‐7 で考えても同じという事になります。
次は ![]() を書き換えると
を書き換えると 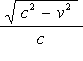 になりますので
になりますので
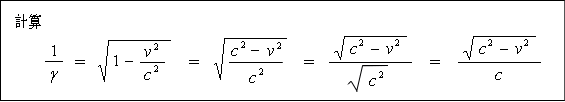
これを 図 2‐4‐7 に当てはめて考えてみましょう。
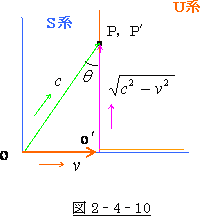
その図を 図 2‐4‐10 とします。
まづP,P′点の所の角度をθ、S系に於ける光速を ![]() 、U系
、U系
の移動速度を ![]() とすれば U 系 内での光の速度は便宜上(数学
とすれば U 系 内での光の速度は便宜上(数学
上)![]() になります。
になります。
そうすると ![]() は cosθ ともなるのです
は cosθ ともなるのです
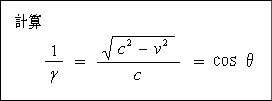
そこで、これを (2-4-4) 式 に戻せば
![]() (2-4-5)
(2-4-5)
となります。
そこから、これは、図 2‐4‐11 の中の三角関数を表わしているのだ
という事が判ってきます。 つまり
![]()
とは、図 2‐4‐11 の中の三角関数の事だったのです。
当然 ![]() の元の式である
の元の式である
![]()
もまた 図 2‐4‐11 の三角関数の式という事になります。
つまり「時間の遅れ」論の元となった式は、本当は、図 2‐4‐11 の中の三角関数を表わしていたわけ
です。
「ちょっと待て、それなら『動いている系の時間は静止系に比べて遅れる』という理屈も成り立つ
ではないか」と言われそうですが、そうは行きません。
なぜなら、この式は ![]() 軸に垂直に発された光のみで考えられているからです。
軸に垂直に発された光のみで考えられているからです。
他の方向の光は一切考慮されていません。他の方向の光で考えたなら、この式は成り立ちません。
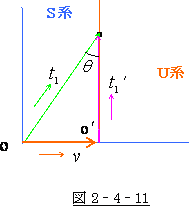
 次に立場を変えて、S系の原点 Oより
次に立場を変えて、S系の原点 Oより ![]() 軸に垂直に発された光を
軸に垂直に発された光を
基準にして考えて見ましょう。
そうすると、図 2‐4‐12 より式は
![]() (2-4-6)
(2-4-6)
となり、全く正反対の結果が生じてしまいます。
この場合、U 系 の方が S系 より時間が進む事になるのです。
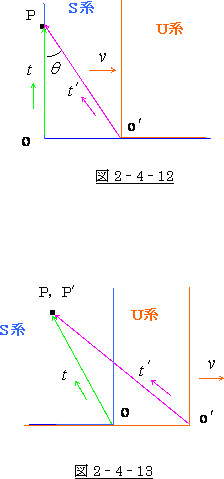
そして、第三に系の進行方向と逆向きに光を発すれば
図 2‐4‐13 の様に ![]() >
> ![]() となりまして、U 系 の時間
となりまして、U 系 の時間
の方が確実に S系 より進む事になります。
というわけで「時間の遅れ」論の理屈は成り立ちません。
尚、図だけの説明では承服しかねるという方の為に、教
科書と同じやり方で、正反対の結果を導き出し、この理論
が誤りである事も証明しておきましょう。
(d) 逆も成り立つ

と、この様になります。
こういう導き方では、やり方次第で、どっちの結果でも得られるのです。
従って「動いている系の時間は遅れる」という理論も誤りとなります。
尚、私が《動いている系での光の速度》を便宜上 ![]() とした事は、ここでは深く考えないで下さ
とした事は、ここでは深く考えないで下さ
い。これは次章の「アインシュタインの論文批判」や第四章の「四次元時空」の所でも出て来ますから。
そして、その時、意味がはっきりして来ます。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る