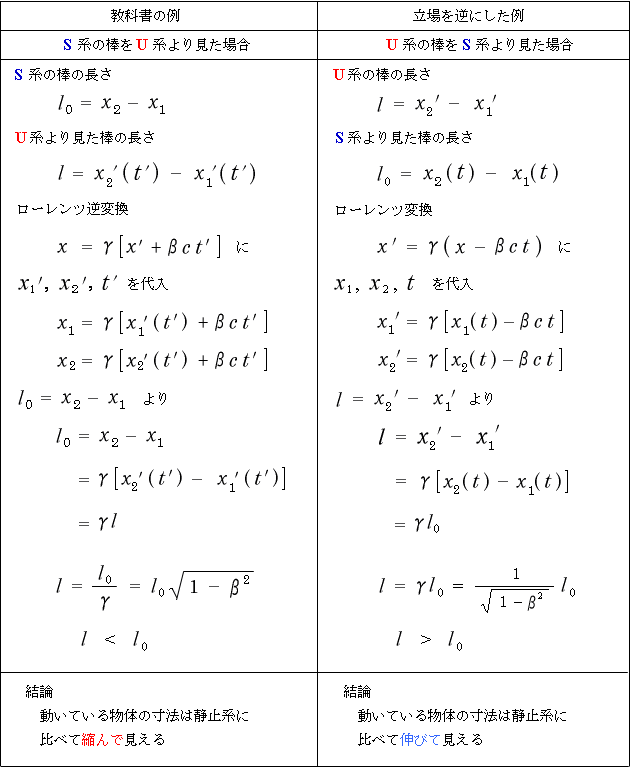(3) ローレンツ収縮の矛盾
(a) ローレンツ収縮の理論の誘導は同時性の理屈と矛盾する
前項の“同時性”では
《静止系の  の異なる二つの場所で 同時に起こったと観測される現象は、
の異なる二つの場所で 同時に起こったと観測される現象は、
動いている系では 同時とは観測されない》
とあった筈です。
ところが、ここ“ローレンツ収縮”のところでは、棒の両端の位置を測定した時の時刻を、静止系だけ
でなく動いている系でまで同じにしています。
これは同時性の理屈に反する事です。
同時性の理屈に照らすなら
《静止系に置いてある棒の両端の位置を、動いている系から 同時に観測したとしても、
その位置は静止系時間では 同時刻の時の位置ではない》
となる筈です。
「それがどうした、時刻が違っても棒の位置が同じなら関係無いではないか!」と言われそうですが、
そうは行きません。なぜなら観測者が動いているからです。
それは立場を引っ繰り返せば、棒が動いているのと同じ事になります。
これが動いていなければ問題無いのですが、 動いているから問題になるのです。
位置が動きますから。
動いている棒の両端の座標を別々の時刻に測ったなら、正しい寸法は出ないでしょう。
同時性の理屈に照らすなら
《動いている棒の両端の位置を、静止系から同時に観測したとしても、その時見えている位置
は、棒の系の時刻で左端が  の時の位置・右端が
の時の位置・右端が 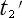 の時の位置》となる筈です。
の時の位置》となる筈です。
それが同時に見えているだけです。
その状態を図示すれば図 2‐3‐7の様になるでしょう。
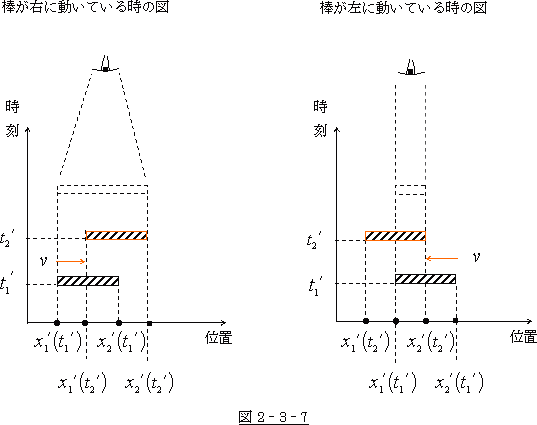
この図でもって、静止系での位置に対応する位置を、動いている系より見ようとするならば、左端
を 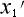 (
(  ) 右端を
) 右端を 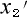 (
( 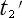 ) としなければなりません。
) としなければなりません。
そうすると、棒の長さは系の進行方向によっては、長く見えたり短く見えたりするかも知れません。
この場合、時刻は重要な要素となります。 関係無いなどと勝手に外せません。
つまり相対論とは、この様に、自説の中にすら矛盾を含んでいる物だったのです。
と言っても、相対論信者の方がこの程度の事で納得される筈もないでしょうし、ローレンツ変換を
導いた時の図 2‐1‐4 から想像して、「それでも長さは縮む」とガリレオ張りの主張をされるでしょう
から、その事についても触れておきましょう。
(b) 光が前に進めば寸法は縮み、光が後ろに進めば寸法は伸びる

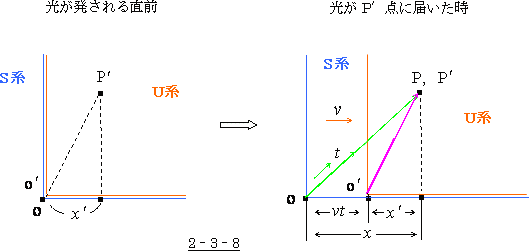
図 2‐3‐8 を見て下さい。光が発される直前には S系 の O 点と  系 の O′点は重なっています。
系 の O′点は重なっています。
そして O,O′点を発した光が  系 のP′点に届いた時、
系 のP′点に届いた時、 系 は距離にして
系 は距離にして 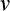
 だけ右に移動して
だけ右に移動して
いますので、S系の距離  は
は  系 の距離
系 の距離  に比べて
に比べて 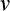
 だけ長くなります。
だけ長くなります。
これは、見方を変えれば  系 の寸法が S 系 に比べ、縮んだという事にもなるわけです。
系 の寸法が S 系 に比べ、縮んだという事にもなるわけです。
そこから考えて“動いている物体の寸法は縮む”という理屈も成り立ちそうな気がしないでもありません
が、事はそう単純ではありません。
物事には裏表があるのです。逆も言えます。
光を系の進行方向と逆向きに発したらどうなるでしょうか。
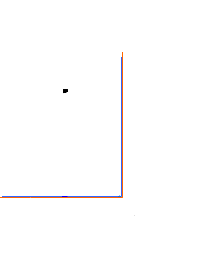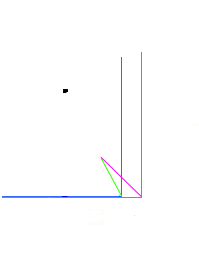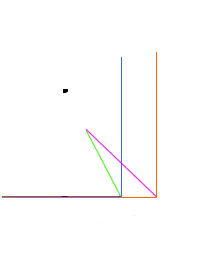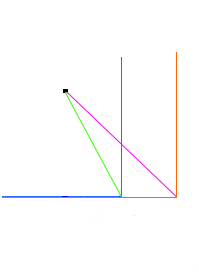
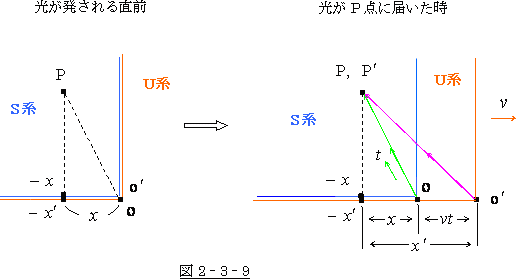
図2‐3‐9を見て下さい。光が発される直前 O点と O′点は重なっています。
そして、光が発されてS系 のP点に届いた時、 系 は
系 は 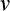
 だけ右に移動していますので
だけ右に移動していますので  系の
系の
距離  は S系の距離
は S系の距離  に比べて
に比べて 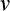
 だけ長くなります。
だけ長くなります。
そうすると今度は、動いている系の寸法の方が静止系より伸びた事になるのです。
光を前に発した時の図では、動いている系の寸法は縮んで見えたのですが、後ろに光を発した時の図
では、逆に伸びて見えるのです。
これは、私が第一章・第二節の「列車の中の時間の矛盾」の所で述べたのと似た現象でしょう。
前に進む光を基準にして考えれば寸法は縮み、後ろに進む光を基準にして考えれば寸法は伸びる。
しかして、一点より発された光は同時に前にも後ろにも進むもの。
こういう場合、寸法は縮みもしなければ伸びもしないと考えるのが妥当でしょう。
これはアインシュタインが変な操作(光速度不変の原理の導入)をしたから、
“光が前に進む部分”で寸法が縮み、その反動として
“光が後ろに進む部分”で寸法が伸びて、
おかしな事になってしまったのです。
ローレンツ収縮は、この誤った操作により生じた所のしわ寄せの“光が前に進む部分”だけを捕らえた
物ですから正しくはありません。全くナンセンスな物となります。
ところで、この「光を後方に発した時の図」は「ローレンツ逆変換」とも関連がありますので、この事
についても触れておきましょう。
(c) 光を前方に発した時と、後方に発した時とでは
静止系と動いている系の立場が逆転する。
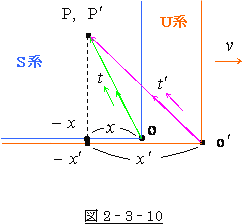
図 2‐3‐10 の様に後ろ向きに光を発すると、P点、P′点の
 ,
,  座標は (−
座標は (− ), (−
), (− ) となりますので、これをローレン
) となりますので、これをローレン
ツ変換
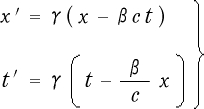 (2-1-8)
(2-1-8)
に代入してみましょう。 そうすると
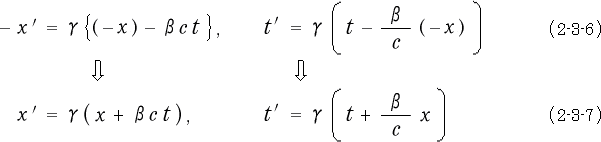
となりまして、ローレンツ逆変換 (2-1-10)

 とよく似た形が出て来ます。ただ
とよく似た形が出て来ます。ただ  と
と  、
、 と
と 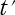 が
が
入れ替わっているだけですけど。
そしてまた、これは、光の方向は元のままで、系の進行方向を
逆にしても同様の結果が得られます。
進行方向を逆にするという事は、速度 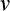 を (−
を (−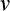 ) にすると
) にすると
いう事ですから、これをローレンツ変換に代入してみます。
すると
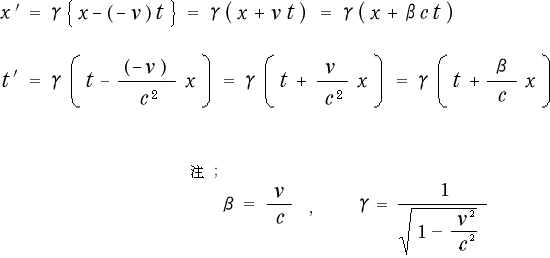
となりまして、これもやはり同じ結果が得られます。
ここでちょっと、逆変換の式と正変換で光の方向と系の方向とを逆にした時の式を並べてみましょう。
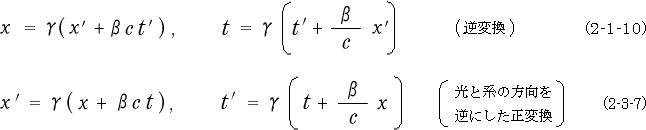
この様に二式は似ています。違うのは  と
と  、
、 と
と 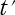 が入れ替わっている事だけです。
が入れ替わっている事だけです。
これは一体何を意味しているのでしょうか。
(2-1-10)式は、光を前方に発した時のS系の  と
と  を表しており、
を表しており、
(2-3-7)式は光を後方に発した時の  系 の
系 の  と
と 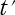 を表していますので、
を表していますので、
これを図にして並べてみましょう。
そうすると
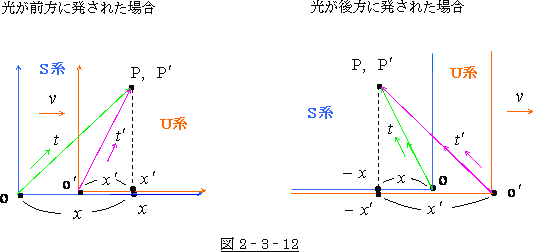
図 2‐3‐12 の様になりまして、両方とも光の経路の長い方を指している事が判ります。
つまり

などの様に、( )の中の記号がプラスになってる式は、図では光の経路の長い方を示し、
逆に

などの様に、( )の中の記号がマイナスになってる式は、図では光の経路の短い方を示して
いたのです。
ここより、光が前方に発せられた時と、後方に発せられた時とでは、S系と  系 の立場が逆転する
系 の立場が逆転する
事が判ります。
図で明らかな様に、
* 光が後方に発せられた時の  系 の光の経路は、光が前方に発せられた時の S系 の光の
系 の光の経路は、光が前方に発せられた時の S系 の光の
経路と相似しており、
* 光が後方に発せられた時の S系 の光の経路は、光が前方に発せられた時の  系 の光の
系 の光の
経路に相似しています。
* 光を後方に発した時の  系 は、一般に相対論で言う所の“静止系”と同じ状態にあり、
系 は、一般に相対論で言う所の“静止系”と同じ状態にあり、
* 光を後方に発した時の S系 は、一般に相対論で言う所の“動いている系”と同じ状態に
あります。
本来はS系が“静止系”で、 系が“動いている系”ですから、ここではS系と
系が“動いている系”ですから、ここではS系と  系のあるべき
系のあるべき
状態が逆転した事になります。
つまり、系の進行方向と逆向きに光を発すると、静止系と動いている系の立場が入れ替わってしま
うのです。
そういうわけですから“静止系”だの“動いている系”だのと言っても意味ありません。光の方向
一つで引っ繰り返りますから。
尚、教科書の理論の誘導の仕方は、それをそっくりそのまま使って、全く逆の結果をも導き出す事
が出来ますので、それも紹介しておきましょう。
(d) 動いている棒の寸法は静止系に比べて伸びる。
ここでは、 系 に置いてある棒をS系より観察するという形で、教科書に書いてある手順をそっくり
系 に置いてある棒をS系より観察するという形で、教科書に書いてある手順をそっくり
そのまま使って、逆の結果を導き出してみましょう。
「 系 で静止している長さ
系 で静止している長さ  の棒を考える。棒は
の棒を考える。棒は  軸に平行に置かれているものとする。
軸に平行に置かれているものとする。
棒の両端の  系 での座標を
系 での座標を 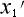 ,
, 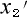 とすると
とすると
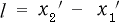
であって、これは  に無関係である。
に無関係である。
この棒をS系 から見たら、その長さはどうなるであろうか。
S系 から見ると棒は速度 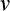 で動いており、その長さは、S系 で同時刻
で動いており、その長さは、S系 で同時刻  に観測した棒の両端の
に観測した棒の両端の
 座標の差により与えられる筈である。S系での長さを
座標の差により与えられる筈である。S系での長さを 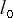 とすると
とすると
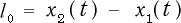
であるが変換(2-1-8)より
 (2-3-8)
(2-3-8)
である事から
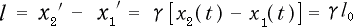 (2-3-9)
(2-3-9)
という関係が得られ
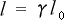 (2-3-10)
(2-3-10)
となる。ところで
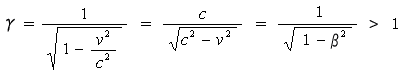 (2-3-11)
(2-3-11)
であるから
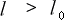 (2-3-12)
(2-3-12)
となり
《U系にある棒の長さはS系より見ると伸びて見える》事になる」となります。
ごまかしていると思われてはいけませんので、これを表の様な形にし、教科書のやり方と併記して
比べてみましょう。
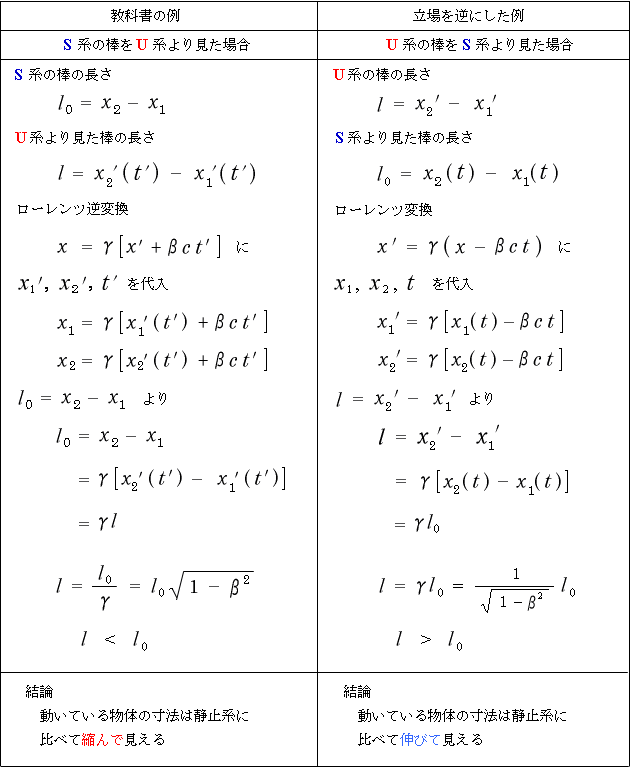
この通り何のごまかしもありません。この様なやり方ではどっちでも成り立つのです。
以上の論証により「ローレンツ収縮」は誤りとなります。
そしてまた、ここより、第一章の「列車の中の時間の矛盾」で述べた事が、私の単なる思いつきで
はなく、相対論の本質に由来する物である事がお解りになると思います。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る






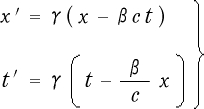 (2-1-8)
(2-1-8)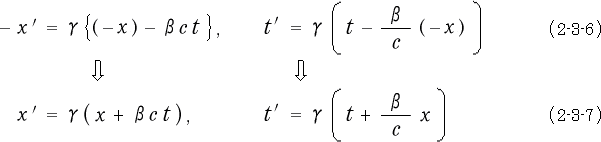


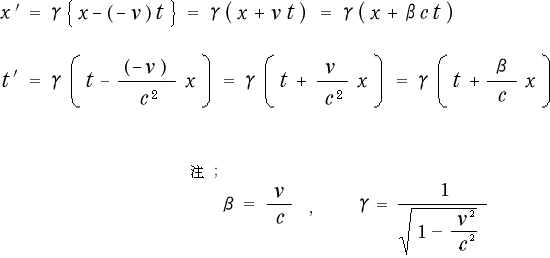
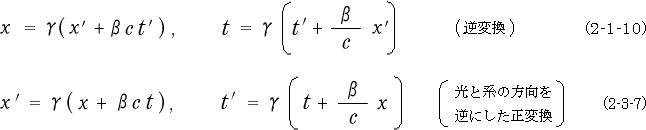


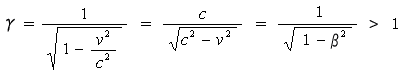 (2-3-11)
(2-3-11)