(4) 動く時計の遅れ(時間の遅れ)
この項に関しましては、前の二つの項とは別の本を採用しています。
その理由は、説の誘導の仕方に納得し難い物が多く、解説がしづらかったからです。
問題は山程あったのですが、それをつついた所で所詮は、執筆者のミスとされるだけで相対論のミス
では無いとされるのが落ちだったので外しました。
ここでは、別の本(原島鮮著『力学』裳華房)に在った分を採用しています。
ただ、この本の原文は、専門書特有の非常に解りづらい書き方がしてありまして(内容は大した事
ないのですが)解説すると不必要にややこしくなりますので、最初から翻訳して紹介する事にしました。
なお原文は、静止系は 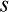 系、動いている系は
系、動いている系は 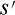 系となっていたのですが、これも、私の文章と
系となっていたのですが、これも、私の文章と
合わせる為に S 系・ 系 とします。
系 とします。
そして、式の番号も私の文章の番号に統一する事にします。
(a) 教科書の内容
教科書では (原文はこちら)
「 
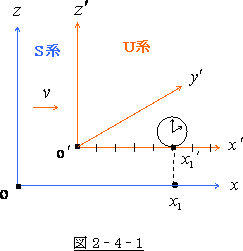 系 の
系 の  軸上のある点
軸上のある点 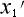 という所に時計が置いてある
という所に時計が置いてある
とする。
この時計は  系 から見ると静止しているのであるが、S 系
系 から見ると静止しているのであるが、S 系
から見ると速度 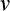 で動いている事になる。
で動いている事になる。
さて、この 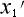 という所で二つの事件が起こったとしよう。
という所で二つの事件が起こったとしよう。
そして、その二つの事件の起こった時刻を  ,
,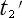
とおこう。
次に、ここに、ローレンツ逆変換(2-1-10)
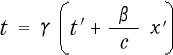
を持って来て、これに  系 での時刻
系 での時刻  ,
,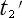 と座標の
と座標の 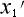 とを代入して、その時の S 系 での
とを代入して、その時の S 系 での
時刻  1 と
1 と  2 とを求めてみよう。
2 とを求めてみよう。
そうすると
 (2-4-1)
(2-4-1)
が得られる。
この得られた  1,
1, 2 よりS系 から見た所の両事件の間の時間間隔を求めてみよう。
2 よりS系 から見た所の両事件の間の時間間隔を求めてみよう。
それは
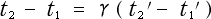 (2-4-2)
(2-4-2)
となる。
ところで、この式の右辺の 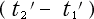 は
は  系 で見た所の両事件の間の時間間隔であるから、
系 で見た所の両事件の間の時間間隔であるから、
 系 をメインにする為に、これを左側に出して
系 をメインにする為に、これを左側に出して
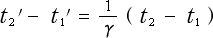 (2-4-3)
(2-4-3)
とおき、この式を言葉で表わして見れば
( 系での時間間隔)=
系での時間間隔)= 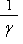 (S系での時間間隔)
(S系での時間間隔)
= 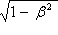 (S系での時間間隔)
(S系での時間間隔)
となる。そして 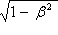 は常に1より小であったから、それをも考慮に入れるとこの式は
は常に1より小であったから、それをも考慮に入れるとこの式は
( 系での時間間隔)<(S系での時間間隔)
系での時間間隔)<(S系での時間間隔)
という事になるのである。
これは『同じ出来事の経過時間でも、U系 で測る方が S系 で測るよりも時間が短い』早い話が
『動いている系での方が静止系でよりも時間の進み方が少ない。つまり、時間が遅れる』」
と言ってるわけです。
確かに、これも文章の流れだけを何の気なしに読むと、そう思わせられます。
しかし、これも間違っています。
(b) 誤りの証明
まず第一に、これも前項と同じ事ですが、ローレンツ逆変換 (2-1-10)
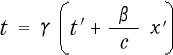
に  系 での二つの時刻
系 での二つの時刻  ,
,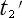 と時計の位置の座標の
と時計の位置の座標の 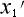 とを代入すれば、S 系 での時刻
とを代入すれば、S 系 での時刻
(  系 での
系 での  ,
,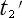 に対応する)が求まると勘違いしている事です。
に対応する)が求まると勘違いしている事です。
この式は、そんな式ではありません。
これは、光の走った所の距離と時間の関係式ですから。
ここの誤りについても詳しく説明していきます。
教科書では  1 ,
1 ,  2 ,
2 ,  ,
,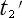 を時刻として設定していますが、それを代入する所のローレンツ
を時刻として設定していますが、それを代入する所のローレンツ
逆変換の  ,
,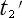 は時刻ではありません。これは光の走行時間です。
は時刻ではありません。これは光の走行時間です。
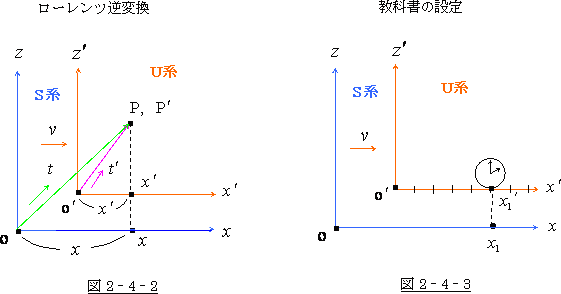
ローレンツ逆変換の  は 図 2‐4‐2 の S 系 に於いて光が O点 から P点 まで走るのに掛かる時間
は 図 2‐4‐2 の S 系 に於いて光が O点 から P点 まで走るのに掛かる時間
ですし、 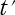 は
は  系 に於いて光が O′点から P′点まで走るのに掛かる時間です。
系 に於いて光が O′点から P′点まで走るのに掛かる時間です。
けっして任意の時刻ではありません。
次に、教科書では 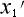 を時計の置いてある位置として、
を時計の置いてある位置として、 軸上の任意の点の座標に設定していますが、
軸上の任意の点の座標に設定していますが、
ローレンツ逆変換の  は任意の点の座標ではありません。
は任意の点の座標ではありません。
これは 図 2‐4‐2 の中の距離の  です。
です。
これは  系 に於いて光が O′点から P′点まで走った所の距離の
系 に於いて光が O′点から P′点まで走った所の距離の  軸方向成分です。
軸方向成分です。
座標と見なしても P′点の  座標に限られます。
座標に限られます。
けっして任意の点の座標などではありません。
その次に、アインシュタインや相対論の専門家が見落としている事に 《ローレンツ変換の  は
は
時間と共に変動する》 という事があります。
ローレンツ変換の  は、
は、  = 0
の時は 0 ですが時間と共に大きくなり
= 0
の時は 0 ですが時間と共に大きくなり  = ∞(無限大)では
= ∞(無限大)では
無限大になります。一定ではありません。
これは  軸上の距離だろうと、P′点の
軸上の距離だろうと、P′点の  座標だろうと同じ事です。
座標だろうと同じ事です。
一方、設定の  は時計の位置ですから動きません。これは不変です。こういう点からも、時計の
は時計の位置ですから動きません。これは不変です。こういう点からも、時計の
位置の  をローレンツ変換の
をローレンツ変換の  に代入する事は間違いなのです。
に代入する事は間違いなのです。
とは言いましても、言ってる事の意味がわからないといけませんので、これを図でもって説明する
事にします。
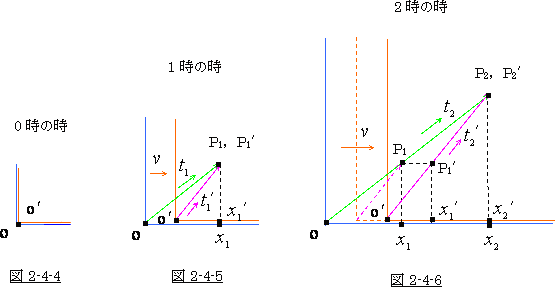
図 2‐4‐4 を見て下さい。
動きの(参照図)
最初 0時の時には、S系 の原点 O と  系 の原点 O′は重なっています。
系 の原点 O′は重なっています。
この時は、まだ光は発されていません。 従って P点・P′点は原点の中にあります。
故に  = 0です。
= 0です。
次に光が 0 時に発射され1時間経った(つまり1時の)時の 図を 図2‐4‐5 とします。
時間がたつにつれ光の走行距離は伸びて行き、2時の時では1時の時のちょうど倍になります。
それが 図2‐4‐6 です。
図でわかります様に、1時の時のP1,P1′点と2時の時のP2,P2′点とでは位置が違います。
当然1時の時の 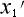 と2時の時の
と2時の時の 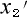 も位置が違います。
も位置が違います。
これがローレンツ変換の  です。
です。
それに対して時計の位置というのは動きませんから、1時であろうと2時であろうと同じ場所です。
この様に時計の位置の  とローレンツ変換の
とローレンツ変換の  とでは意味が違うのです。
とでは意味が違うのです。
あー、それから、「光が一時間走ったら、とんでもない距離で、こんな比較なぞ出来ないぞ」という、
厳密な議論はやめて下さいね。これはあくまでも、単純化した話ですから。
というわけで、同じ位置での時間経過を云々する問題にローレンツ変換を使う事は出来ません。
ローレンツ変換は光の走った距離と時間の関係式ですから。
光の到達時刻が変われば到達位置も異なって来ます。
時刻は進んでいるのに、位置をそのままというわけには行きません。
そこの所の違いに気づかず混同して使うとおかしな事になります。
もっとも、そうは言いましても、このローレンツ変換の  と時計の位置の
と時計の位置の  とを一致させる
とを一致させる
方法が無いわけでもありません。
そこで、次はそれをやってみて、相対論の式が本当は何を言っているのかを調べてみましょう。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る

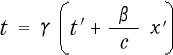
 (2-4-1)
(2-4-1) 
