棒の両端のS系 の座標を
これは「動いている物体の寸法は、静止系から見ると実際より縮んで見える」という説です。
S系 で静止している長さ ![]() の棒を考える。棒は
の棒を考える。棒は ![]() 軸に平行に置かれている物とする。
軸に平行に置かれている物とする。
棒の両端のS系 の座標を ![]() ,
,![]() とすると
とすると
![]() (2-3-1)
(2-3-1)
であって、これは ![]() に無関係である。
に無関係である。
この棒を速度 ![]() で動いている
で動いている ![]() 系 から見たらその長さはどうなるであろうか。
系 から見たらその長さはどうなるであろうか。
![]() 系 から見ると棒は速度 −
系 から見ると棒は速度 −![]() で動いており、その長さは
で動いており、その長さは ![]() 系 で同時刻
系 で同時刻 ![]() に観測した
に観測した
棒の ![]() 座標の差により与えられる筈である。
座標の差により与えられる筈である。![]() 系 での長さを
系 での長さを ![]() とすると
とすると
![]() (2-3-2)
(2-3-2)
であるが、変換 (2-1-10) により
![]() (2-3-3)
(2-3-3)
である事から
![]() (2-3-4)
(2-3-4)
という関係が得られ
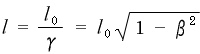 (2-3-5)
(2-3-5)
となる。従って ![]() 系 から見た棒の長さは
系 から見た棒の長さは ![]() の割合いで収縮して見える。同様に
の割合いで収縮して見える。同様に ![]() 系 で
系 で
静止している ![]() 軸に平行な棒の長さは、S系 から見ると
軸に平行な棒の長さは、S系 から見ると ![]() の割合いだけ収縮して見える。
の割合いだけ収縮して見える。
となっています。
これも、良く解からないと思われますので補足して説明します。
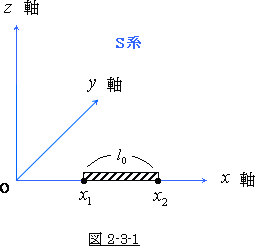
まず、S系 に置いてある長さ ![]() の棒を考えます。この棒
の棒を考えます。この棒
は ![]() 軸に平行に置かれてある物とします。
軸に平行に置かれてある物とします。
棒の両端の座標を ![]() ,
, ![]() とすれば、その長さは
とすれば、その長さは
![]()
で表わされます。
ところで、この棒を速度 ![]() で動いている
で動いている ![]() 系 から見た
系 から見た
ら、どう見えるでしょうか。
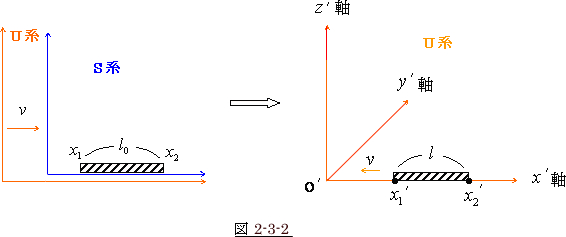
![]() 系 から見ると、棒の方が速度 −
系 から見ると、棒の方が速度 − ![]() で、つまり反対方向に動いている事になります。
で、つまり反対方向に動いている事になります。
そして、その長さは ![]() 系 で同時刻
系 で同時刻 ![]() に観測した所の棒の
に観測した所の棒の ![]() 座標の差により与えられる筈です。
座標の差により与えられる筈です。
そこで、棒の両端の座標を ![]() ,
, ![]() と置いてみましょう。そうすると、その長さは
と置いてみましょう。そうすると、その長さは
![]()
で与えられる事になります。
次に、ここに、ローレンツ逆変換(2-1-10) の
![]()
を持って来て、これに ![]() 系 より観測した所の棒の両端の座標
系 より観測した所の棒の両端の座標 ![]() ,
, ![]() と時刻の
と時刻の ![]() とを代入
とを代入
して、S系での棒の両端の座標 ![]() と
と ![]() を求めてみましょう。
を求めてみましょう。
そうすると
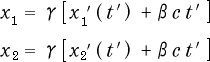
が得られます。そこで、この得られた座標 ![]() ,
, ![]() よりS系 に於ける棒の長さを求めてみます。
よりS系 に於ける棒の長さを求めてみます。
棒の長さ ![]() は
は ![]() −
− ![]() ですから、
ですから、
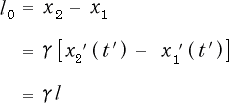
となります。ところで、この式の最後を良く見て下さい。最後の ![]() は
は ![]() 系 より見た所の棒の長さ
系 より見た所の棒の長さ
です。従って、この結果より《 S系 での棒の長さ》と《 ![]() 系 より見た所の棒の長さ》との間には
系 より見た所の棒の長さ》との間には
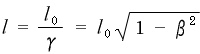
( 注; 1/γ = ![]() については 式(2-1-9)を参照 )
については 式(2-1-9)を参照 )
という関係のある事がわかります。
そこで、この式を素人にも解かる様に言葉に置き換えてみましょう。そうすると、それは
( ![]() 系 より見た棒の長さ)=
系 より見た棒の長さ)= ![]() ×( S系 での棒の長さ)
×( S系 での棒の長さ)
となります。
ところで相対論では ![]() は常に1より小ですので、
は常に1より小ですので、

この結果は
( ![]() 系 より見た棒の長さ)<( S系 での棒の長さ)
系 より見た棒の長さ)<( S系 での棒の長さ)
という事になるのです。 そうすると、これは
《 静止している棒を、動いている系から眺めた場合、その長さは、静止系で見るのに比べて
![]() の割合で縮んで見える 》
の割合で縮んで見える 》
という事になり、それはまた逆の見方として
《動いている棒を静止系から眺めても、同様に縮んで見える》
という理屈にもなるわけです。そして、ここより
《動いている物体の寸法は、これを静止系から眺めると、本来の寸法より縮んで見える》
という結論が得られるのです。
これが、ローレンツ収縮の理屈です。
これも、何の気なしに読むと、数式の解る人なら「なるほど!」と思わせられます。
しかし、これも間違っています。
(C) 誤りの証明
まず第一の間違いはローレンツ逆変換 (2-1-10) の
![]()
に ![]() 系 での棒の両端の座標
系 での棒の両端の座標 ![]() ,
, ![]() と時刻の
と時刻の ![]() とを代入すれば、S系 での棒の両端の座標
とを代入すれば、S系 での棒の両端の座標
![]() ,
, ![]() が求まると勘違いしている事です。
が求まると勘違いしている事です。
この式は、そんな事のための式ではありません。
これは、光の走った距離と時間の関係式ですから。
次に教科書が設定している所の
![]() ,
, ![]() ,
, ![]() ,
, ![]() は棒の両端の座標ですが、これを代入する
は棒の両端の座標ですが、これを代入する
所のローレンツ逆変換の ![]() ,
,![]() は棒の両端の座標ではありません。
は棒の両端の座標ではありません。
これは、光の到達点の ![]() ,
,![]() 座標です。しかして、その実体は光の走行距離の
座標です。しかして、その実体は光の走行距離の ![]() ,
,![]() 軸方向
軸方向
成分なのです。
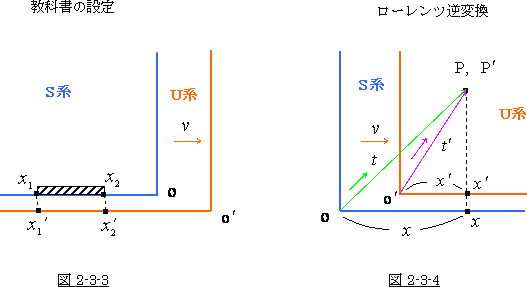
具体的に申しますと、![]() は静止系に於いて光が走った所の距離 OP の
は静止系に於いて光が走った所の距離 OP の ![]() 軸方向成分ですし、
軸方向成分ですし、![]() は
は
動いている系に於いて光が走った所の距離 O′ P′の ![]() 軸方向成分です。
軸方向成分です。
これを座標と解釈しても図 2-3-4 の中の P,P′点の ![]() ,
,![]() 座標に限られます。
座標に限られます。
けっして、棒の両端の座標などではありません。
次に、ローレンツ逆変換の ![]() ,
,![]() もまた光の走行時間でして、任意の時刻ではありません。
もまた光の走行時間でして、任意の時刻ではありません。
そういうわけですから、ローレンツ逆変換をこのような設定に用いる事は出来ません。
これは、間違っています。
そうは言いましても、こういう意見に対しましては
「棒の両端の位置を図 2-3-4 の中に P1点, P2点として置けば問題無いのでは」
とおっしゃる方があるかも知れませんので、そうすればどうなるかを、やってみましょう。
棒の両端の位置を静止系の 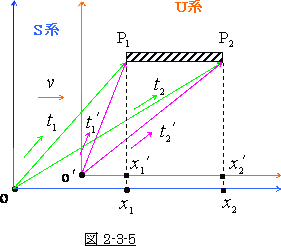 P1
P1 ![]() 点 、
点 、
P2 ![]() 点の位置に置きます。
点の位置に置きます。
そして、棒は ![]() 軸に平行ですから
軸に平行ですから
![]() 1 =
1 = ![]() 2 ,
2 , ![]() 1 =
1 = ![]() 2
2
とします。
そうして図を作りますと、それは、図2-3-5 の様になります。
ところが困った事に、ここでも
![]() 1 =
1 = ![]() 2 ,
2 , ![]() =
= ![]()
とはなりません。
これは前項と同じ問題です。
設定では「これは ![]() に無関係で」とありましたが、ローレンツ変換を用いる限り無関係とは
に無関係で」とありましたが、ローレンツ変換を用いる限り無関係とは
なりません。
設定の ![]() は系全体の時刻ですが、ローレンツ変換の
は系全体の時刻ですが、ローレンツ変換の ![]() は光の走行時間です。
は光の走行時間です。
場所が違えば光の到達時刻も違ってきます。当然、時刻は一致しません。
故に、 ![]() 1 =
1 = ![]() 2,
2, ![]() =
= ![]() とはなりません。
とはなりません。
そうするとβ![]() ′の項が消えませんから、式 (2-3-4) は
′の項が消えませんから、式 (2-3-4) は
![]()
ではなく
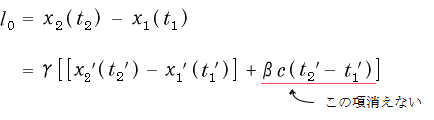
としなければならなくなります。
ところが、そうすると、結論の ![]() が出て来ませんから、ローレンツ収縮の理論も
が出て来ませんから、ローレンツ収縮の理論も
生まれて来なくなります。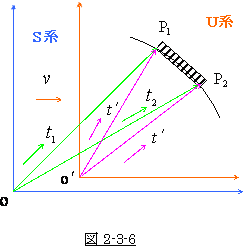
それでは不都合ですので β![]() ′の項が消える様に
′の項が消える様に ![]() 系
系
での時刻が一致する所、![]() 系 の原点 O′より同一半径の球
系 の原点 O′より同一半径の球
面上に P1点 と P2点 とを置いて見ましょう。
図 2-3-6 のようにすれば ![]() 系 での光の走行距離は一定です
系 での光の走行距離は一定です
から、光の到達時刻は P1点でも P2点でも同じになります。
従って、動いている系での時刻も一致します。
ところが今度は、棒の方が ![]() 軸に平行ではなくなってし
軸に平行ではなくなってし
まいます。
その上、S系 の時刻も一致しません。
つまり、この様に矛盾を生じてしまうのです。
かつ、ここの問題は前項の“同時性”の理屈に抵触して来ます。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る