二、式の誤りの続き
前章では、相対論の誤りについて「光速度不変の原理」には根拠が無い事と、「光速度絶対」は式を
解いた結果そうなったのではなく、最初から、そういう前提で式が建てられていたのだという事を説明
しました。
しかし、この程度の事では相対論の専門家は納得しないでしょう。
そこで、これらの事は良しとしても、なおかつ、他に、多くの問題や間違いの有る事を紹介します。
相対論の中には各論として
＊「静止系の二カ所で同時に起こった出来事でも、それを動いている系から見ると、同時とは見えない」
とか
＊「動いている物体の寸法は、それを静止系から見ると縮んで見える」とか
＊「動いている系の時間は静止系に比べて遅れる」
等という珍妙な説が沢山あります。
ところが、これらは全て間違っているのです。
その原因は、アインシュタインが式の意味を間違って解釈した事にありました。
彼は自分が作った式の意味を正しく理解していません。
その為、話がトンチンカンな事になり奇想天外・摩訶不思議な方向へと行ってしまったのです。
一体、何が間違っているのか、どこがおかしいのか、それを解(わ)かってもらうには、その前に、
式の意味を知ってもらう必要があります。そこで、ここでは、ローレンツ変換の誘導過程を復習
しながら、前章よりもう少し詳しく説明して行く事にします。
その後で各論の問題点を検証して行く事にしましょう。
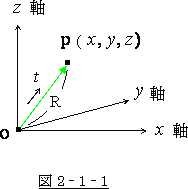
まず、図2‐1‐1の様な直交座標系を考えます。
この座標系のある点 Ｐ( 
) に原点 
より光が進んだと
しましょう。
そうすると、その距離 Ｒ は光速を 
、走行時間を 
として
(2-1-1)
で求まります。
ここで、既に が任意の時刻ではなく、光の走行時間である事が、はっきりして来ます。
次に光が走った所の Ｐ 間の距離 Ｒ を、Ｐ点 の座標より求めて見ましょう。
ピタゴラスの定理より Ｒ の二乗は
(2-1-2)
ですので、これを開平しますと
(2-1-3)
になります。この部分は計算上必要なかったので前章では省きました。
ここで「 はともかく、距離 Ｒ を Ｐ点の座標より求めたのなら は座標ではないか」
と言われる方があるかも知れませんので説明します。
まずは、ピタゴラスの定理からです。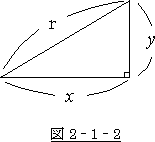
図 2‐1‐2の様な場合、ピタゴラスの定理は
(2-1-4)
です。
ここでは 
も 
も 
も辺の長さですから距離です。
座標でない事は言うまでもありません。
では三次元の場合はどうなるのでしょうか。
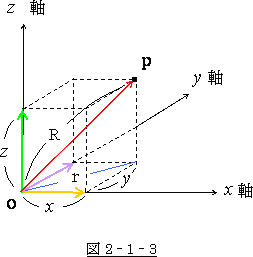図 2-1-3 の様な場合、OＰ 間の距離を R としますと、
ピタゴラスの定理は
(2-1-5)
となります。そして
ですから
(2-1-2)
となります。
この場合 は辺の長さですから全て距離です。 元は座標だったとしても (2-1-2) 式の
中では距離となるのです。
(2-1-2) 式は本当は
（2-1-6)
( 距離 )2 ( 距離 )2 ( 距離 )2 ( 距離 )2
と書くべき所ですが、面倒なので 0 が省かれているだけです。
座標は、カッコの中の と 0, と 0, 
と0 に当たります。
（2-1-6) 式より0 を省けば
（2-1-7)
( 距離 )2 ( 距離 )2 ( 距離 )2 ( 距離 )2
となりますが、これはあくまでも距離の式です。
次に もまた距離の関係式です。
距離 速度 時間
ですから。
そういうわけで、この二式を合成して出来た
(1-4-3) 式
は、当然のことながら、距離の関係式となります。 故に
もまた、距離の関係式となるのです。
次に、この式は距離と時間の関係式でもありますから、これらの式より導かれたところの
ローレンツ変換
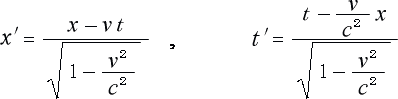
は、当然のことながら、距離と時間の関係式という事になります。
従って、ローレンツ変換の , 
は距離であり , 
は時間なのです。
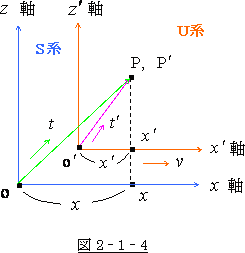
ローレンツ変換が 図 2‐1‐4 の中の関係式であり、距離
と時間の関係式である事は既に説明しました。
そこで、ここでは細かい所を説明して行きましょう。
ローレンツ変換の とは 図 2‐1‐4 の中の距離の
の事です。
これは光が 
系の原点 O′からＰ′点まで走った所の
距離の 軸方向のベクトル成分です。
かつＰ′点の 座標でもあります。
次に ですが、これは 図 2‐1‐4 の中の距離の の事です。これは光が Ｓ系の原点 Oより
U系 のＰ′(Ｓ系のＰ）点まで走った時の距離の 軸方向のベクトル成分です。
かつＰ点の 座標でもあります。
その次に、 とは 系において、光がO′点よりＰ′点まで進むのに掛かる時間ですし、
とはＳ系において、光がO点からＰ点まで進むのに掛かる時間です。
これを解かりやすくする為に一覧表の様な形にまとめてみましょう。
そうすると、それは表１の様になります。
| |
系の距離 O′P′の 軸方向成分、かつＰ′点の 座標 |
| |
Ｓ系の距離 OＰの 軸方向成分、かつＰ点の 座標 |
| |
系において、光が O′Ｐ′間を進むのに掛かる時間 |
| |
Ｓ系において、光が OＰ間を進むのに掛かる時間 |
 |
Ｓ系 に対する 系 の移動速度 |
| |
光速 |
表 １
ここより、式の意味を説明しますと
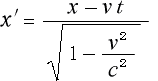
とは、 系での光の走行距離の 軸方向成分を
Ｓ系での光の走行距離の 軸方向成分とＳ系での光の走行時間
とで以って表わした物で、
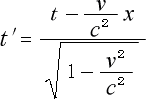
とは、 系での光の走行時間 を
Ｓ系での光の走行時間 とＳ系での光の走行距離の 軸方向成分
とで以って表わした物
という事になります。
つまりローレンツ変換とは、Ｓ系の や を変数に使って、 系の や を表わした物
という事になるのです。
なお、ローレンツ変換
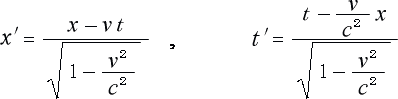
は、このままでは繁雑ですので
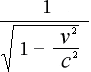を γ に、
を β に置き換えて
（2-1-8）
という形で用いられています。
注；
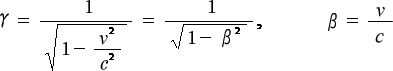(2-1-9)
γ（ガンマ）、β（ベータ）はギリシャ文字
次に、ローレンツ変換には逆変換として
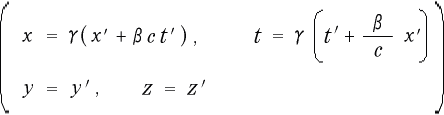(2-1-10)
というのもあります。
これは、動いている系の や を変数に使って、静止系の や を表わした物です。
この式は、各論の証明の時に頻繁に出て来ます
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る