(二) 各論の誤りの証明
準備段階が終わりましたので、次よりは各論の問題点に入ります。
各論のテーマは「同時刻の相対性」、「ローレンツ収縮」、「時間の遅れ」についてです。
これらについては、何が問題なのかをはっきりさせる為に、教科書の記述をそのまま紹介します。
しかしながら、学校の教科書というのは、えてして、解かりにくく書いてある物でして、そのまま
では、何を言ってるのかよく解かりません。
そこで、原文の後に解説した文章をつけ、その後で、問題を論評する事にします。
なお、教科書では静止系は K系、動いている系はK′系となっていたのですが、これは私の文章の
都合上、S系・ 系 と変え、式の番号も私の文章の番号にそろえる事にします。
系 と変え、式の番号も私の文章の番号にそろえる事にします。
それ以外は手を加えません。
(1) 同時性(同時刻の相対性)
これは「静止系の二カ所で同時に何かが起こったとしても、それを動いている系から見ると、
同時とは見えない」という話です。
(a) 教科書では
S系の 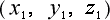 と
と 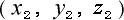 という二つの点で同時刻
という二つの点で同時刻  に起きた出来事は、
に起きた出来事は、
 系 では一般に同時ではなくなり
系 では一般に同時ではなくなり 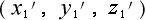 で時刻
で時刻  に
に 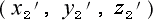
で時刻 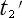 に起きたと観測される。 変換 (2-1-8) から
に起きたと観測される。 変換 (2-1-8) から
 (2-2-1)
(2-2-1)
となるから
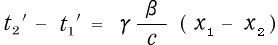 (2-2-2)
(2-2-2)
となって 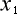 =
= 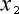 でない限り
でない限り 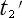 =
=  とはならない。すなわち S系 で
とはならない。すなわち S系 で  の異なる
の異なる
二つの場所で同時に起こったと観測される現象が、 系 では同時とは観測されないのである。
系 では同時とは観測されないのである。
(原文はこちら)
となっています。
この文章では、はっきり言って、何を言ってるのか良く解かりませんので解説します。
(b) 解説
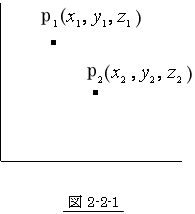 まず、静止系の中に P1
まず、静止系の中に P1 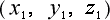 点 と P2
点 と P2 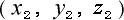 点
点
という二つの場所を置きます。
そして、この二つの場所で同時に何かが起こったと仮定します。
その時の時刻を  としましょう。
としましょう。
次に、この現象を動いている系から目撃したとします。
その時の  系 での時刻を
系 での時刻を
P1 点 については 
P2 点 については 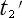
と仮に置いてみます。
そうしておいて、ここに、ローレンツ変換(2-1-8)
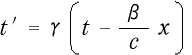
を持って来、これに S系 での時刻  とS系での二カ所の座標
とS系での二カ所の座標 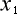 と
と 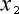 とを代入して
とを代入して  系 での
系 での
時刻  と
と 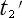 とを求めて見ましょう。 そうすると、それは
とを求めて見ましょう。 そうすると、それは
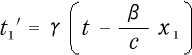 (2-2-3)
(2-2-3)
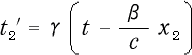 (2-2-4)
(2-2-4)
となります。
ここでもし、 系 の二カ所の時刻が同じであるならば
系 の二カ所の時刻が同じであるならば 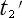 −
−  =0 になる筈です。
=0 になる筈です。
そこで、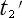 より
より  を引いてみます。 ところが、結果は
を引いてみます。 ところが、結果は
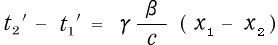 (2-2-2)
(2-2-2)
となりまして、必ずしも 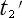 −
−  = 0 とはなっていません。
= 0 とはなっていません。
この式で 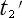 −
−  が 0 となるのは
が 0 となるのは 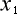 =
= 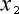 の時だけです。
の時だけです。
そこより「 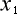 =
= 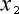 でない限り
でない限り 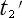 =
=  とはならない」となり、
とはならない」となり、
「同じ場所でない限り、 系 では同じ時刻とはならない」という考え方が生まれて来たわけです。
系 では同じ時刻とはならない」という考え方が生まれて来たわけです。
それは言い換えれば「静止系の  の異なる二カ所で同時に何かが起こったとしても、
の異なる二カ所で同時に何かが起こったとしても、
それを動いている系から見れば同時とは観測されない」という事になるわけです。
これが「同時性」の理屈です。
言われてみれば、「確かに」、「なるほど」、と思えて来ます。
しかしながら、これは間違っています。
(c) 誤りの証明
まず第一に、ここではローレンツ変換の
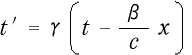
にS系での時刻  とS系での二カ所の座標
とS系での二カ所の座標 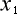 と
と 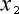 とを代入して、
とを代入して、 系 での時刻
系 での時刻  と
と 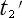
とを求めていますが、誰が、この式をそんな風に使えると決めたのでしょうか。
この式は、そんな事の為の式ではありません。
ローレンツ変換は光が走った所の距離と時間の関係式なのです。
 これから、その間違いを具体的に説明していきます。
これから、その間違いを具体的に説明していきます。
教科書の設定では  ,
,  ,
, 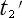 は任意の時刻となっています。
は任意の時刻となっています。
しかしながら、これを代入する所のローレンツ変換の  ,
, 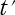 は
は
任意の時刻ではありません。
これは、光の走行時間です。
 は S系 において、光が O点から P点 まで走るのに掛かる
は S系 において、光が O点から P点 まで走るのに掛かる
時間ですし
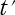 は
は  系 において、光が O′点から P′点まで走るのに
系 において、光が O′点から P′点まで走るのに
掛かる時間です。
次に 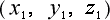 ,
,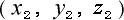 ,
,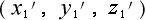 ,
,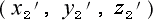 ですが、
ですが、
これも教科書の設定では任意の点の座標となっていますが、
これを当てはめる所のローレンツ変換の  は任意の点の座標ではありません。
は任意の点の座標ではありません。
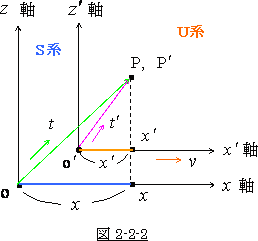
これは、図 2-2-2 の中の距離の  です。
です。
これは、S系において光が走った所の距離 OPの  軸方向成分です。
軸方向成分です。
座標と解釈しても P点の  座標に限られます。
座標に限られます。
決して任意の点の座標などではありません。
従って、ローレンツ変換を教科書の様な設定で使う事は出来ません。
これは間違いです。
とこう申しますと、こういう異論に対しましては
「 “光が、時刻=0の瞬間に原点Oを発し、時刻  の時にP点に届いた”と解釈す
の時にP点に届いた”と解釈す
れば  を時刻とみなしても良いのではないか?
を時刻とみなしても良いのではないか?
図 2-2-2 の中では、P点は自由にとれるのだから、ここで設定している所の点を
図 2-2-2 の中にP点として置けば問題は無かろう」
とおっしゃる方があるかも知れませんので、そうやったら、どうなるのかをやってみましょう。
まず設定では、二つの点 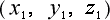 と
と 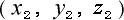 とがありますので、
とがありますので、
これを P1, P2 点として 図 2-2-2 の中に任意に置きます。
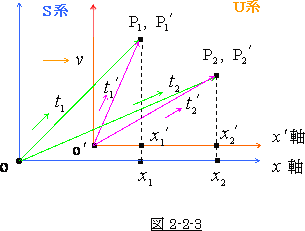 そうすると、それは、図 2-2-3 の様になります。
そうすると、それは、図 2-2-3 の様になります。
ところが、ここで問題が生じます。
設定では  は静止系全体の時刻の筈です。
は静止系全体の時刻の筈です。
従って P1 点 でも P2 点 でも時刻は同じでなければなり
ません。
ところが、図 2-2-3で明らかな様に
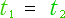
とはなっていません。
ローレンツ変換の  は、元々、光の走行時間ですから、これを光の到達時刻と置き換えても、
は、元々、光の走行時間ですから、これを光の到達時刻と置き換えても、
系全体の時刻とはならないのです。
P1 点 と P2 点 の位置が違えば、光の走行距離が違いますから、到達時刻も違って来ます。
従って 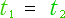 とはなりません。
とはなりません。
ローレンツ変換の  を時刻とみなせば、静止系の中ですら異なる位置の時刻は異なる事になって
を時刻とみなせば、静止系の中ですら異なる位置の時刻は異なる事になって
困った事になります。
そういうわけで、ローレンツ変換の  を時刻に
を時刻に  を座標とみなしても、うまく行かないのです。
を座標とみなしても、うまく行かないのです。
では全く駄目なのかと言うとそうでもありません。
(d) 式の意味の勘違い
実は、このやり方でも“同時刻の相対性”の理屈を成り立たせる方法があるのです。
それには、どうすれば良いのか。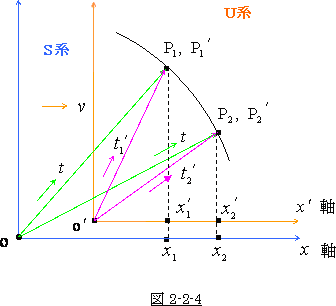
それには、まず、静止系の時刻が一致する所、つまり
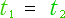 となる所を探し出し、そこに P1点 と P2点
となる所を探し出し、そこに P1点 と P2点
とを置く事です。
その位置は静止系の原点Oから同一半径の球面上です。
ここにP1点とP2点とを置けば、静止系での光の到達
時刻は皆同じになります。距離が同じですから。
かつ、動いている系での光の到達時刻は一致
しません。
従って、ここでなら式 (2-2-2) の
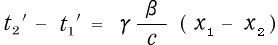
は成り立ちます。
そして、ここでなら「静止系の  の異なる二カ所で同時に何かが起こったとしても、それを動い
の異なる二カ所で同時に何かが起こったとしても、それを動い
ている系から見れば同時とは観測されない」という理屈はこじつけられます。
「同時性(同時刻の相対性)」とは、実は、こういう特殊な条件下で成り立つ式の意味を間違って
解釈した物だったのです。
確かに、こういう限定条件下でなら、そういう理屈も成り立つでしょう。
しかしながら、これは、この球面上でのみ成り立つ理屈ですから正しくはありません。
球面を一歩でも外に出たら最後、静止系ですら同一時刻は存在しません。
そうなると、任意の場所に自由に座標を設定する事も出来なくなります。
つまり、 この様に矛盾を生じてしまうのです。
これでは、一般性を持ちません。
従って、同時性の理論は誤りとなります。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る
 (2-2-1)
(2-2-1)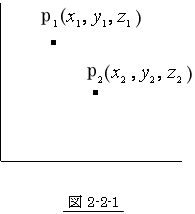
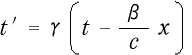
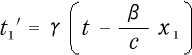
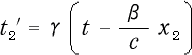 (2-2-4)
(2-2-4)

