「次に静止系では時間
静止系の時刻が
その場所を
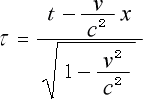 (3-5-1)
(3-5-1)また、
という関係がある。
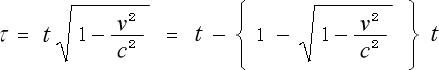 (3-5-3)
(3-5-3)となる。それ故に静止系で考えると、静止系の時間の一秒毎に、走っている時計は
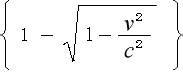 秒づつ遅れる事になる」
秒づつ遅れる事になる」とあります。 (原文はこちら)
「次に静止系では時間 ![]() を示し、運動系では時間
を示し、運動系では時間 ![]() を与える時計を考えよう。
を与える時計を考えよう。
静止系の時刻が ![]() の時、運動系の原点に固定されている時計が時刻
の時、運動系の原点に固定されている時計が時刻 ![]() を示し、
を示し、
その場所を ![]() とすれば、変換公式により
とすれば、変換公式により
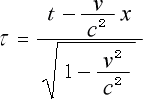 (3-5-1)
(3-5-1)
また、![]() と
と ![]() との間には
との間には
![]() (3-5-2)
(3-5-2)
という関係がある。
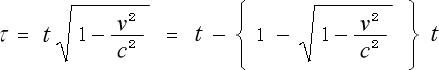 (3-5-3)
(3-5-3)
となる。それ故に静止系で考えると、静止系の時間の一秒毎に、走っている時計は
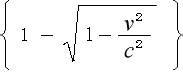 秒づつ遅れる事になる」
秒づつ遅れる事になる」
とあります。 (原文はこちら)
これも言葉が省略されすぎて解かりにくいので、言葉を補って説明します。
「運動系の原点 O′に時計が固定されているとします。
そして静止系の時刻が ![]() の時に、運動系の時計が時刻
の時に、運動系の時計が時刻 ![]() を示しているとしましょう。
を示しているとしましょう。
この時運動系の原点 O′は、静止系の ![]() 軸上の或る点
軸上の或る点 ![]() の所に在ったとします。
の所に在ったとします。
ローレンツ変換より ![]() と
と ![]() の間には
の間には
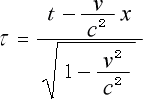
 という関係のある事が分かっています。
という関係のある事が分かっています。
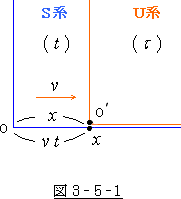
そして ![]() と
と ![]() との間には、静止系と運動系の位置を示す 図 3‐5‐1
との間には、静止系と運動系の位置を示す 図 3‐5‐1
より
![]()
という関係のある事も分かっています。
そこで、この ![]() の
の ![]() を式 (3-5-1) に代入して
を式 (3-5-1) に代入して
みますと
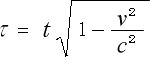 (3-5-4)
(3-5-4)
となります。ここでこの結果を少し細工して
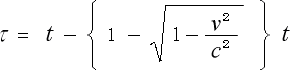 (3-5-5)
(3-5-5)
とおいて見ましょう。そうすると、この結果より運動系にある時計は、静止系時間の一秒毎に
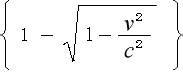 秒づつ遅れる事になる。」
秒づつ遅れる事になる。」
と言ってるわけです。
この論文も数式の流れだけを見ていると、うっかりその気にさせられます。
しかし、これも間違っています。
まず第一の不自然な事は
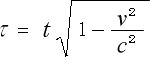 (3-5-4)
(3-5-4)
という結論の式を出してから、これを小細工して
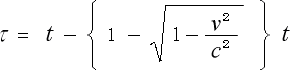 (3-5-5)
(3-5-5)
とし、この結果で以て、運動系の時間は静止系の時間の一秒毎に 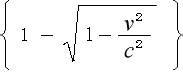 秒づつ
秒づつ
遅れるとした事です。
しかしながらアインシュタインは、最初 ![]() と
と ![]() を任意の時刻としていた筈です。
を任意の時刻としていた筈です。
だったら 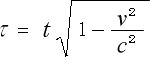 は時刻の関係式でしょう。
は時刻の関係式でしょう。
ところが、次には、これを細工して一秒毎に 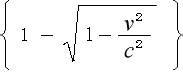 秒づつ遅れるとしました。
秒づつ遅れるとしました。
でも、そうすると 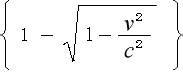 は経過時間いう事になってしまいます。
は経過時間いう事になってしまいます。
つまり、ここでは ![]() と
と ![]() を経過時間として取り扱っているのです。
を経過時間として取り扱っているのです。
時刻が、いつ、経過時間にすり替わったのでしょうか。
この式 (3-5-4)でもって経過時間を求めたいのなら ![]() −
− ![]() という形にしなければなりません。
という形にしなければなりません。
そうではなく、ただ小細工しただけの式なら、まだ時刻の関係式のままでしょう。
![]() と
と ![]() を時刻として設定したのなら
を時刻として設定したのなら
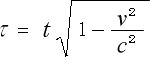
は、あくまでも時刻の関係式でなければなりません。
そうすると、ここでの ![]() と
と ![]() の違いはU系の時刻とS系の時刻の違いという事になります。
の違いはU系の時刻とS系の時刻の違いという事になります。
それは、東京の時刻が ![]() の時にロンドンの時刻が
の時にロンドンの時刻が ![]() であるという程度の違いにしかなりません。
であるという程度の違いにしかなりません。
日本が12時の時、イギリスは3時ですから、アインシュタイン流のやり方で行けば、イギリスの
時間は日本に比べて1日に9時間の割合で遅れている事になります。
別に間違いではありません。
ただ、これは、時間の遅れと言うより時差ですけど。
イギリスの時計が日本に比べて9時間遅れで時を刻んでいるのは確かです。
しかし、別にイギリスの時計の時を刻む速度が、日本に比べて1日に9時間の割合で遅れている
わけではありません。
アインシュタインのやっている間違いとは、実は、こういう間違いなのです。
アインシュタインは時刻のずれと、時間の進行速度の違いとを混同しています。
アインシュタインは時刻と時間を混同しているから、こういう間違いを犯すのです。
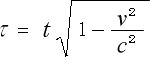
をローレンツ変換本来の意味で用いれば、![]() と
と ![]() は光の走行時間ですから、この式は問題なく
は光の走行時間ですから、この式は問題なく
《時間の遅れ》の式になります。
そうしないのは、アインシュタインが ![]() と
と ![]() を時刻と思い込んでいたからでしょう。
を時刻と思い込んでいたからでしょう。
次に、本文では「 ![]() と
と ![]() との間には、
との間には、![]() という関係がある」というくだりが
という関係がある」というくだりが
ありましたが、これも問題です。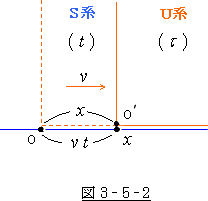
前にも申しました様に、この節で最初に設定された ![]() は、
は、
S系空間に於ける任意の時刻です。
それに対して ![]() の
の ![]() とは U系の原点 O′が
とは U系の原点 O′が
S 系の原点 O の所から ![]() 軸上を移動して座標
軸上を移動して座標 ![]() の所
の所
まで行くのに掛かる時間です。
最初の設定の ![]() は、S系空間の任意の時刻ですが、
は、S系空間の任意の時刻ですが、
![]() の
の ![]() は U系の移動時間なのです。
は U系の移動時間なのです。
この二つの ![]() は何の関係もありません。全くの別物です。
は何の関係もありません。全くの別物です。
それなのにアインシュタインは、両者がまるで同一の物であるかのように扱っています。
これも、彼が時刻と時間とを混同している事から起こる事でしょう。
本来なら、この二つの ![]() は別々の記号で表わさなければなりません。
は別々の記号で表わさなければなりません。
S系空間の時刻を ![]() で表わすのなら、U 系の移動時間は T で表わすとか。
で表わすのなら、U 系の移動時間は T で表わすとか。
そうしないから、区別がつかず混同してしまうわけです。
もっとも、「S系の時刻で ![]() =0 の時に U系 の原点と S系 の原点とが重なっていた」
=0 の時に U系 の原点と S系 の原点とが重なっていた」
という条件でも付ければ話は別ですが。
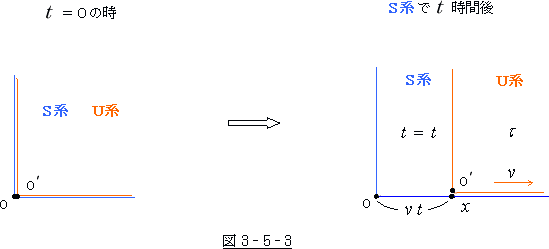
その時は、U 系の移動時間 T をS系の時刻 ![]() でもって代用する事が出来ますので
T と
でもって代用する事が出来ますので
T と ![]() を
を
同じ物と見なす事が出来ます。
しかしながら、ここには、その様な条件は何もついていません。
従って、![]() の
の ![]() とローレンツ変換の
とローレンツ変換の ![]() とが同じ物であるという保証はどこにも有りません。
とが同じ物であるという保証はどこにも有りません。
もっとも、それを言ってしまうと話がここで終わってしまい、他の問題を追窮できなくなりますので、
アインシュタインが忘れたという事にして話を進めます。
次にアインシュタインは
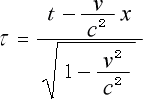
の ![]() に
に ![]() の
の ![]() を代入しようとしていますが、
を代入しようとしていますが、
なぜ、そうしなければならないのでしようか。その必然性と根拠が示されていません。
本来、この二つの ![]() は別物で代入できる様なしろ物ではありません。
は別物で代入できる様なしろ物ではありません。
ローレンツ変換
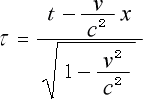
の ![]() とは 図 3‐5‐4(下図↓) の中の距離の
とは 図 3‐5‐4(下図↓) の中の距離の ![]() の事です。
の事です。
これは、光が静止系の原点 O からP点まで走った時の距離の ![]() 軸方向成分です。
軸方向成分です。
座標と見なしてもP点の ![]() 座標に限られます。
座標に限られます。
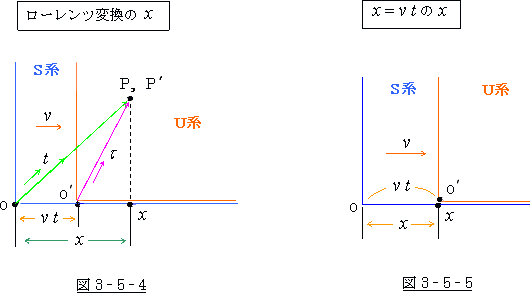
それに対して、![]() の
の ![]() とは 図 3‐5‐5 の中の距離の
とは 図 3‐5‐5 の中の距離の ![]() です。
です。
これは、U 系の原点 O′が S系の ![]() 軸上を
軸上を ![]() 時間掛けて移動した時の距離です。
時間掛けて移動した時の距離です。
座標と見なしても U 系原点の S系 ![]() 軸上に於ける位置にしかなりません。
軸上に於ける位置にしかなりません。
この二つの ![]() は何の関係もありません。どうして代入出来るのでしょうか。
は何の関係もありません。どうして代入出来るのでしょうか。
それともアインシュタインは ![]() の
の ![]() を時計の位置と見、これを
を時計の位置と見、これを
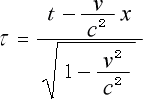
に代入すれば、U系での時刻が出て来るとでも考えていたのでしょうか。
もしそうだとしたら、これは、とんでもない勘違いです。
この式は、そういう式ではありませんから。
ローレンツ変換は、光の到達位置と到達時刻の関係式なのです。
時計の位置や空間の時刻を求める式などではありません。
また、仮に、百歩譲ってそうだったとしても、ここに新たな問題が生じて来ます。
それは「同時性」との絡みからです。
同時性の理屈では「静止系の二箇所で同時に何かが起こったとしても、
それを動いている系から見ると同時とは見えない」となっていた筈です。
静止系では同時刻であっても、動いている系から見ると原点とその他の場所とでは時刻が異なって
いる事になっています。
そして、この式は最初の設定により運動系の原点を基準にして作られています。
そうすると、原点を基準にして「時間の遅れ」の式を作ったとしても、それを、原点以外の場所には
適用できません。
ありとあらゆる場所で時刻体系が異なっていますから、一つとして共通の式は創れなくなります。
この様に矛盾を生じて来るのです。
もっとも、そうは言っても、アインシュタインのやり方で理屈の成り立つ所が無いわけでも
ありませんので、次は、そこの所を検討してみましょう。
まずは前に戻って
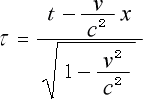
の ![]() に
に ![]() の
の ![]() を代入する件を座標と言う観点から見直してみましょう。
を代入する件を座標と言う観点から見直してみましょう。
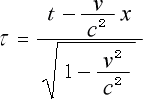
の ![]() とは静止系で光が到達した所の点Pの
とは静止系で光が到達した所の点Pの ![]() 座標 (図3-5-6) です。
座標 (図3-5-6) です。
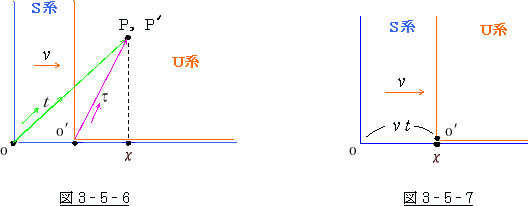
そして、 ![]() の
の ![]() とは、U 系 原点のS系
とは、U 系 原点のS系 ![]() 軸上に於ける位置 (図3-5-7) です。
軸上に於ける位置 (図3-5-7) です。
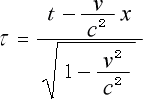
の ![]() に
に ![]() の
の ![]() を代入するという事は、この二つの
を代入するという事は、この二つの ![]() を一致させるという事です。
を一致させるという事です。
それには、どうすればよいのか。
 それには、光の到達点であるP点を、U 系 原点 O′より
それには、光の到達点であるP点を、U 系 原点 O′より
![]() 軸に垂直に引いた線上に持って来る事です。
軸に垂直に引いた線上に持って来る事です。
そうすれば要求された状態になります。
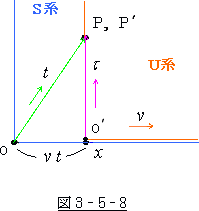
そしてそれを図で表わせば 図 3-5-8 の様になります。
これは、前章(教科書)の“時計の遅れ”の所で示した
「U 系 に於いて、原点O′より ![]() 軸に垂直に光を発し、
軸に垂直に光を発し、
それをS系から眺めた時の 図 2-4-7 と同じでしょう。
U 系 の原点 O′より光を ![]() 軸に垂直に発し、それを
軸に垂直に発し、それを
S系より眺めれば、光の到達点の ![]() 座標は常に U 系 原点の在る場所と同じになります。
座標は常に U 系 原点の在る場所と同じになります。
従って、この時に限り、アインシュタインの設定は成り立ち、結論の式
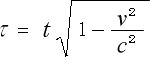
も成り立ちます。当然アインシュタインの理論も成り立ちます。
しかしながら、これは、![]() 軸に垂直に発された光のみで考えられている事であって、
軸に垂直に発された光のみで考えられている事であって、
他の方向の光は一切考慮されていませんから、正しくは有りません。
他の方向の光で考えたなら、この式は成り立たなくなります。
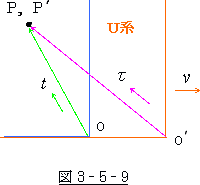 それどころか、光を系の進行方向と逆向きにでも発すれば
それどころか、光を系の進行方向と逆向きにでも発すれば
![]() >
> ![]()
となって、運動系の時間が静止系より進んでしまいます。
尚、これより先は、前章の「時間の遅れ」と同じに
なりますので、論証は省略します。
ともかく、そういうわけで、「動いている時計の遅れ」説も
間違いとなるのです。
この項に関する限り、教科書のやり方とアインシュタインのやり方は、それ程、違っていません。
文章の表面だけを見ていると、全く、違っている様に見えたのですが、本質的には同じ事だったのです。
ここまでの論証で明らかな様に、一見、教科書の執筆者の間違いに見える様な事でも、突きつめて
行けば、その根がアインシュタインにあった事が判ってきます。
アインシュタインがそういう間違いをしていたから、他の先生方も、気づかず追随してしまったと
言うべきです。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る