アインシュタインは、最初に《同時刻についての定義》を定めました。
これは“二箇所の時刻が同時刻であるかどうかをどうやって判定するか”というものです。
一般に時刻は時計で計られます。しかし遠く離れた場所では、その時計同士が合っているという
保証は有りません。そこでアインシュタインは、次の様な方法で時計が合っているかどうかを判定
する事にしました。
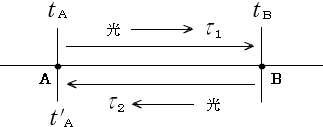
まず Ａ点 と Ｂ点 とに一個づつ時計を置き、Ａ点 より Ｂ点 に向けて光を発射し、Ｂ点 で反射
させて Ａ点に戻します。
これまでの論証は、私が大学で習った所の教科書に沿っての物でした。
ところがアインシュタインの原文（翻訳物）は、こうはなっていませんでした。
やり方が全く違っていたのです。
余りにも式が少なく、ほとんどが「‥‥と仮定しよう」「‥‥となる筈だ」という言葉の羅列で、
仮定と推測あるいは決めつけで成り立っている様に見えました。
式が余りにも少ない為、式と式との続がりがよく見えず、理解に苦しむ面も多かったのですが、後ろ
の補注や解説を参考にしながら読んでいく内に、この論文にも誤りのある事が見えて来ました。
これは前に、教科書の間違いに気づいていなかったら判らなかった事です。
この論文を翻訳された先生は
「中学生でもわかる初等数学を使って、相対性理論の根幹とも言える重要な公式を導いている。
その説明は、出発点となる前提から目指す結論に至るまで、両者を結ぶ最短コースをたどって、
実に平明な、しかし説得力あふれる論旨で、読者をゴールまで引きずっていく。
この論文は物理学の模範として、それを志す者は必ず一読すべきである。」
とほめちぎっておられます。(原文はこちら)
しかし私には、そうは見えません。非常に杜撰な論文に見えます。
問題は「最短コースをたどって、平明な説明」をしている所です。
この時、思いつきや似た物との混同で読者を勘違いの世界に引きずり込んでいます。
またこの論文では、ローレンツ変換の誘導の所で、式が省略されすぎていて、なぜ、これがこうなる
のか解からない所がありました。
私の頭が悪いと言ってしまえばそれまでですが、この先生自身「難解な所がある」と断って、後ろに
補注や解説をつけておられるくらいです。
ところが、その解説ですら本文の式の流れとは全く無関係に書かれてあり、その先生独自のやり方で
後半を導き出しておられるのです。
そうなると「なんで、これが、こうなるのか？」という私の疑問は解けません。
その先生も、もしかしたら、式の途中をつなぐ事が出来なかったので、やむを得ず、自分流のやり方で
結論を導かれたのではないかと疑ってしまいます。
もっともこれは、ゲスの勘繰りという物で、先生自身は解かっておられたのだが、我々下々の者に
解かる様なレベルの式では表せないので、やむを得ず別の方法をとられたのかも知れません。
その様な不十分な論文を多くの先生方が寄ってたかって、解かりやすく且(か)つ論理的で整合性の
あるキチンとした形に仕上げ直していったのでしょう。
もちろん、その改良の大部分は、アインシュタインの生きている内に行われたでしょうから、アイン
シュタインの承認の下で行われた事は、間違いないと思われます。
私が大学で習った所の相対論は、その様にして改良され体系立てられたものだったのでしょう。
だから原文とは違うのだと思います。
アインシュタインの論文は、はっきり言って解かりにくい、そこで論文をそのまま紹介するのはヤメに
して、私の解かる範囲で問題のある所を抜粋し、それを解説してから論評する事にします。
（原文はこちら)
アインシュタインは、最初に《同時刻についての定義》を定めました。
これは“二箇所の時刻が同時刻であるかどうかをどうやって判定するか”というものです。
一般に時刻は時計で計られます。しかし遠く離れた場所では、その時計同士が合っているという
保証は有りません。そこでアインシュタインは、次の様な方法で時計が合っているかどうかを判定
する事にしました。
まず Ａ点 と Ｂ点 とに一個づつ時計を置き、Ａ点 より Ｂ点 に向けて光を発射し、Ｂ点 で反射
させて Ａ点に戻します。
図 3-1-1
その時に Ａ点 での発射時刻 
A と Ｂ点 での反射時刻 B と Ａ点 に光が戻って来た時の時刻
とを測定しておきます。
そうしておいて、これらのデータより、光の往きの走行時間 
と還りの走行時間 
とを算出
します。
（注； 
はギリシャ文字でタウと発音する）
そうすると、それは
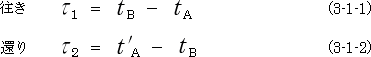
となります。
これは同じ距離を往き来しただけですから、本来 と は同じ値の筈です。
従って、Ａ，Ｂの時計が合っていれば
(3-1-3)
とならなければなりません。
もしならなかったら時計が合っていないという事です。
そういう事からアインシュタインは
を以て、二つの時計が合っている事の根拠としました。 ここまでは、問題ありません。
次にアインシュタインは、動いている棒の上でも同様の思考実験をしました。
（イ）本の原文では
「長さ 
A B の棒があり、その両端を Ａ，Ｂ とする。そして棒の両端に、それぞれ一個の時計を
とりつける。この時計は静止系でキチンと合わせてある物とする。
時刻 A に Ａ から光線が発射され、時刻 B に 点Ｂ で反射され、時刻 にこの光は
Ａ に立ち戻ったとする。これに光速度不変の原理を用いれば次の関係が成立する。
（これは静止系から見た場合の関係式である）
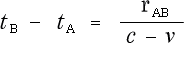(3-2-1)
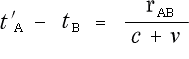(3-2-2)
上の関係式を見ると、棒と一緒に走っている観測者から見るときＡ，Ｂ二つの時計は合って
いない。 そこで、ある座標系から見たとき、二つの事件が同時刻であったとしても、動いて
いる他の座標系からそれを見れば、同時刻に起こったと見なすわけには行かない。」
とやっています。 (原文はこちら)
この部分は「同時刻の相対性」の最初の論文ですが、必要事項が抜けていて解かりにくいので、
補って説明します。
長さ A B の棒があり、その両端をＡ，Ｂとします。この棒は速度 
で 
軸方向をＡからＢの
方向へ動いている物とします。
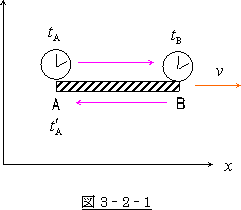
次に、棒の両端にそれぞれ一個の時計を取り付けます。
この時計は静止系でキチンと合わせてある物とします
Ａ端での時刻 A の時に Ａ端より光が発射され、
Ｂ端での時刻 B の時に Ｂ端で反射されて、
Ａ端での時刻 の時に光が Ａ端に戻って来たとします。
この様子を静止系から見ると図3‐2‐2の様になります。これは、
棒の動きと光と時刻との関係を示した物です。
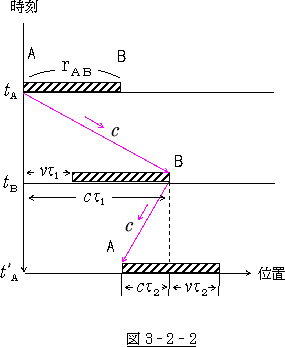この図より、静止系から見た場合の光の走行距離を求
めますと
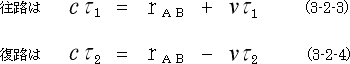
（注； 
は棒の長さ）
ですが
光の往きの走行時間
光の還りの走行時間
ですから、それを考慮に入れますと、(3-2-3)、(3-2-4)式は
往路 
(3-2-5)
復路 
(3-2-6)
となります。
この式より、往路・復路の光の走行時間を求めますと
往路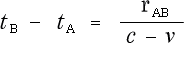
復路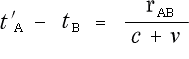
となるわけです。これがアインシュタインの (3-2-1),(3-2-2)式です。
ところが、ここで問題が生じます。
この結果は とはなっていません。
そこで、アインシュタインは自分の作った《同時刻の定義》に照らし合わせて
「静止系で同時刻を示していた二箇所の時計でも、動いている系にあれば同じ時刻を示さない」
即ち
《静止系の二箇所で同時に起こった出来事でも、これを動いている系から見ると同時とは見えない》
と断じたわけです。
しかし、これは間違っています。
アインシュタインはとんでもない勘違いをしています。 前項に於いて《静止系》で
が成り立ったのは、光が往きも還りも同じ距離を走ったからです。
同じ距離を同じ速度で走れば所要時間が同じになるのは当然でしょう。
ところが、今回の《動いている系》では、光の往きと還りの走行距離は同じではありません。
距離が違えば走行時間が違ってきても仕方がないでしょう。
が成り立たないのはそのせいです。 時計のせいではありません。
図3‐2‐2 でわかる様に、
光は往路は棒の長さよりも長く走り、復路は棒の長さよりも短く走っています。
それでいて光の速度を往きも還りも同じとしたら、往きと還りの走行時間が違って来ても
仕方がないでしょう。
往きは、Ｂ点が逃げるので光が追いつくのに時間が掛かり、還りはＡ点が近寄って来たので結果と
して短い時間で戻ってしまった。ただそれだけの事です。
これはアインシュタインのやり方が間違っているのです。
アインシュタインは「静止系でも動いている系でも光の速度は同じ」としました。
その結果「動いている棒上で発された光」でも「往きと還りの速度を同じ」
とせざるを得なくなったのです。
ところが、そうすると、棒の上では光は往きも還りも同じ時間で往復しているのに、
これを外から見ると、光は往きは棒の上よりも長い時間を掛けて走り、還りは棒の上よりも短い時間
で戻る事になってしまいます。
棒の上の時間 (3-1-3)
棒の外の時間 
(3-2-7)
往き 還り
これは非常に不自然な事です。これでは不都合ですので、
やり方を変えて、棒の外の時間 を絶対とし 棒の上の時間 が変化する様にして見ましょう。
そうすると今度は、棒の上の時間は、光が往きの時は外よりも遅れ、戻りの時は外よりも進む
事になってしまいます。
これも不都合ですが、これは私が第一章の「列車の中の時間の矛盾」の所で示した
「光を前方に発すれば動いている系の時間は遅れ、後方に発すれば進む」というのと似た現象でしょう。
ここより第一章の所で私が示した問題は、単なる私のデッチ上げではなく、
その根がアインシュタインに有った事が判って来ます。
それは、ともかく、こういう原因で光の往きの走行時間と還りの走行時間とが異なってしまい
とは、ならなくなってしまったのです。
決して、時計のせいではありません。
これは、単に、アインシュタインのやり方が間違っているだけの話です。
ここで、アインシュタインのやり方の間違いを理解して頂く為に、次の様な例で説明して行く事に
しましょう。
Ａ地点にライトを設置し、そこより東に光を発射させＢ地点で反射させて戻って来させるとします。
その間、観測者（本来、静止系の観測者であった）が西の方へ一定の速度で移動しているものとします。
これは静止系と動いている系の立場を入れ替えただけの話です。
光がＡ地点を発した時刻 A に、たまたま観測者がそこにいて、この光景を目撃したとします。
そして光がＢ地点に届いた時刻 B には観測者は tB 地点の所に移動しています。
その次に、光がＡ地点に戻って来た時観測者は更に移動して 
地点の所にいます
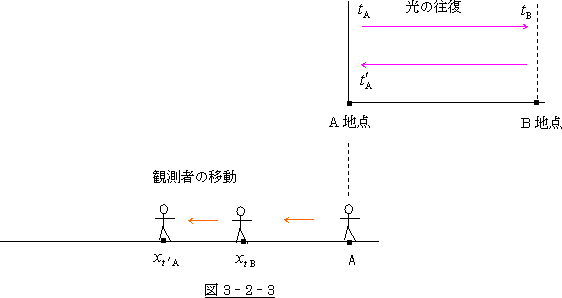
さて、この場合、動いている観測者は、光が tB 地点や 地点より発されたと言う
でしょうか。絶対に言わないでしょう。
この人は、あくまでも、光はＡ地点より発されたと言う筈です。しかるに、観測者に、光は
tB 地点や 地点から発されたと言わせているのが相対論なのです。
相対論では、光の発生原点は観測者と共に動いているかのようです。
これが何の目印もない宇宙空間でしたなら、そういう錯覚をするかも知れません。
が、しかし、目印の多い地上ではそうは行きません。
次に、観測者が静止していて、棒の方が動いている状況で考えて見ましょう。
Ａ地点に観測者が立っていて、動いている棒のＡ端がＡ地点に差し掛かった時、たまたま、棒の
Ａ端より光が発せられたなら、観測者はＡ地点で光が発せられたと思い込むでしょう。
しかし、これは勘違いというものです。
本当は、光は棒のＡ端から発せられたのであって、Ａ地点から発せられたわけではありません。
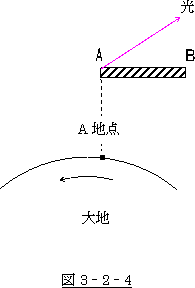棒の方が静止していて、大地の方が動いていると考えたなら、
棒のＡ端が光を発した時、たまたまＡ地点が、そこを通り掛かった
だけという事になります。
次の瞬間には、Ａ地点は別の所に移動しているわけです。従って
「Ａ地点から光を発して」と言うわけには行きません。
さて、そこで《光の往路と復路とで走行距離と走行時間とが異な
る》という問題を“棒が動かず、観測者が動いている”という状況
に置き換えて考えてみましょう。
棒が静止していると考えるのなら光の移動は単にＡＢ間の往復だけです。
問題は動いている観測者の方にあります。
広い宇宙空間に棒と観測者だけがあり、
観測者は自分が動いているとは知らず、棒が動いていると勘違いしているものとします。
棒のＡ端から光が発せられた時、観測者は、たまたま、Ａ地点にいてこれを目撃します。
（注；この時、棒のＡ端はＡ地点に在ったとする）。
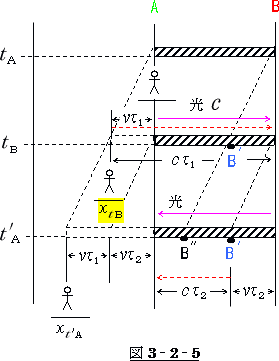
そして光が棒のＢ端に届いた時、観測者は
だけ移動して tB 地点の
所にいるのですが、この人は、自分が動いている
とはつゆ程も知りませんから、光は tB 地点
から発せられて、Ｂ地点で棒のＢ端に届いたと
錯覚しています。
そこで光の進んだ距離は
と計算します。
次に、光がＡ端に戻って来た時、観測者は、更に、
だけ左に移動している
のですが、この人は、自分が動いているとは全く知りませんから、棒の方が、更に
だけ右に移動したと勘違いをします。
そこで、光が反射された時、棒のＢ端はＢ′地点の所に在って、光はその位置より反射されて
Ａ端に戻って来たと思い違いをするわけです。
そうすると、光の復路の走行距離は
になってしまいます。
そこで観測者は、往路は光の走行距離が伸び、復路は短縮されてしまったと考え込むわけです。
しかしながら、これは、観測者が、自分が動いているとは知らず、棒が動いていると錯覚して
いるからこうなるだけです。
実際には、光は棒の両端を一定の時間で往復したに過ぎません。
光は tB 地点で発せられたわけでもなければ、Ｂ′地点で反射されたわけでもないのです。
これは観測者の勘違いから来る物です。
こういう状況では観測者は、自分の動いた距離さえも、光の走行距離に加えてしまいます。
その結果、光の走行距離が伸びたり縮んだりして見えるわけです。
そこの所の勘違いが解かれば《 観測者が静止していて、棒の方が動いている 》という状況でも
《 棒が静止していて、観測者が動いている 》という状況に置き換えてみる事により、
矛盾なく説明する事が出来ます。
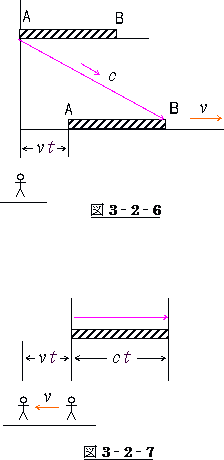
例えば、図3‐2‐6の様に《 速度 で右方向に動いている棒の
Ａ端より発された光がＢ端に届いた 》場合でも、Ａ地点に
静止している観測者の見た、光の“みかけの走行距離”は
《 棒が動かず、観測者が速度 で反対方向に動いている 》と
置き換えてみる事により「棒の上を光が走った距離
」と
「観測者が動いた距離 
」との合計で表わす事が出来ます。
それを式で表わせば
(3-2-8)
です。が、これはまた
(3-2-9)
でもありますから、この式は
（棒の外から見た光の速度）＝（光速）＋（棒の速度）
をも表わしている事になります。
これは、旧来の考え方による速度の合成と一致します。
これが正しいあり方なのです。
アインシュタインは《静止系から見た光のみかけの移動距離》を《棒上での光の移動距離》に
《棒の移動距離》を加えた物としました。
その為、光の《往きの走行距離》が伸び《還りの走行距離》が縮んでしまったわけですが、
一方で彼は《静止系より見た所の光のみかけの速度》を《往き》も《還り》も同じにしています。
これは不自然な事です。
そんな事をしたら、《静止系より見た所の光の往きの走行時間》は《棒上での時間》よりも長くなり、
《還りの時間》は《棒上での時間》よりも短くなって、混乱を来します。
これは無茶苦茶なやり方です。
静止系より見た「光のみかけの移動距離」を「棒上での光の移動距離」＋「棒の移動距離」とした
のなら、「光のみかけの速度」も「棒の上での光速」＋「棒の移動速度」としなければなりません。
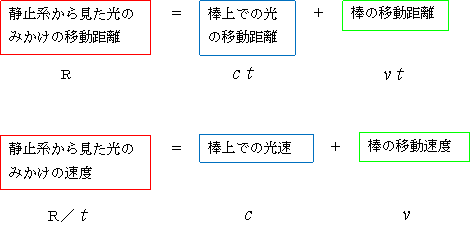
ですから。
そうしなければ、数式的に辻褄が合わないでしょう。
そうしないから《静止系より見た所の光の往きの走行時間》が《棒上での時間》よりも長くなり、
ひるがえって《還りの走行時間》が《棒上での時間》よりも短くなって、不自然な状態になってしまった
のです。
往きと還りの時間が一致しないのは時計のせいではありません。
単に、アインシュタインのやり方が間違っているだけの話です。
アインシュタインの「同時刻の定義」は静止系では成り立ちますが、動いている系では成り立ちません。
そういうわけで、ここより導かれた所の 《静止系の二箇所で同時に何かが起こったとしても、これを
動いている系から見ると同時刻とは見えない》という「時刻の相対性」の理屈も間違いとなります。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る