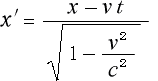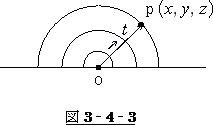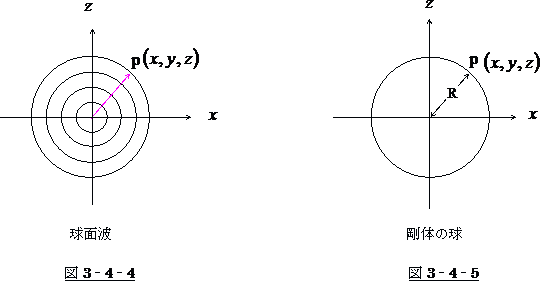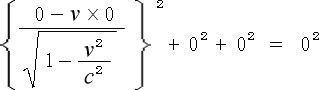(ハ)長さが縮む説の誤りの証明
まず第一の誤りは、動いている球の表面の式を
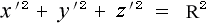
(注;ギリシャ文字ではわかりにくい )
( ので教科書風に書き換えています)
と運動系の座標で表した後、これにローレンツ変換を代入した事です。
ローレンツ変換の 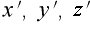 は剛体の球の表面の座標などではありません。
は剛体の球の表面の座標などではありません。
これは、光の球面波の到達点の座標です。
正しくは、光の走行距離の  軸方向成分、
軸方向成分、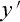 軸方向成分、
軸方向成分、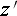 軸方向成分なのです。
軸方向成分なのです。
ローレンツ変換は、光の到達時刻や到達点の座標の関係式ではあっても、任意の時刻や任意の座標の
関係式等ではありません。
従って、この様な応用は出来ません。間違いです。
次に、ここでは (3-4-6) 式
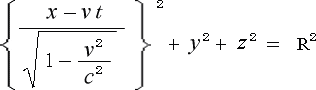
に  =0を代入して
=0を代入して
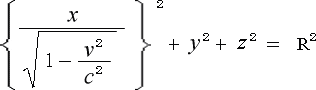 (3-4-2)
(3-4-2)
としていますが、なぜ  =0を代入しなければならないのでしょうか。
=0を代入しなければならないのでしょうか。
本文には 静止系の時刻  =0 の瞬間に、この方程式を静止系から見れば とあるだけで、
=0 の瞬間に、この方程式を静止系から見れば とあるだけで、
その理由や必然性が示されていません。
では別の時刻だったらどうなるのでしょうか。
これを、代入する前のローレンツ変換で考えてみましょう。
ローレンツ変換は
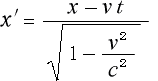
でした。
これに、 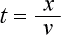 を入れてみましょう。そうすると
を入れてみましょう。そうすると  は0になります。
は0になります。
次に、 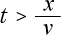 を代入すると
を代入すると  はマイナスになります。
はマイナスになります。
この式では  の値次第で
の値次第で  が変動してしまうのです。
が変動してしまうのです。
これでは、剛体の球の半径(  方向のみ)は時間によっても変動する事になってしまいます。
方向のみ)は時間によっても変動する事になってしまいます。
これは不都合でしょう。
《剛体の球の  軸方向の長さが時間によって変動する》なんて話は聞いた事がありません。
軸方向の長さが時間によって変動する》なんて話は聞いた事がありません。
それが正しいのなら  =0 を勝手に代入するなど出来ません。
=0 を勝手に代入するなど出来ません。
代入するには、明確な条件が必要となります。
条件無しで0を代入できるのは、 がどんな値であろうと径の長さが影響を受けない時だけでしょう。
がどんな値であろうと径の長さが影響を受けない時だけでしょう。
こういうやり方では「動いている球の  軸方向の寸法が縮む」という理論を創り出す前に
軸方向の寸法が縮む」という理論を創り出す前に
「 軸方向の寸法が時間によって変動する」という別の理論を生じてしまいます。
軸方向の寸法が時間によって変動する」という別の理論を生じてしまいます。
それでは不都合ですので、 に0を代入して
に0を代入して  の項を消し、問題を消してしまおうと考えたので
の項を消し、問題を消してしまおうと考えたので
しょうが、実に、無責任です。
その前に「  の文字の入った式」を代入した事自体に問題があると気づくべきでした。
の文字の入った式」を代入した事自体に問題があると気づくべきでした。
本当の問題は代入したローレンツ変換にあるのですから。
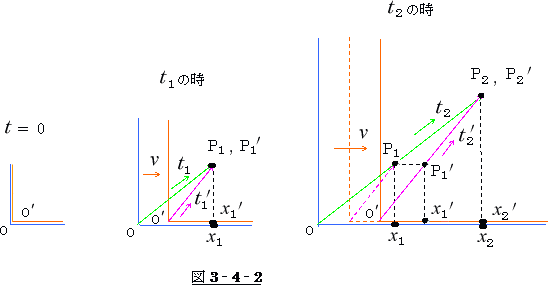
図 3-4-2 で明らかな様に、ローレンツ変換の  は時間と共に大きくなります。
は時間と共に大きくなります。
「動く剛体の球の  軸方向の寸法が縮む」という理論も、この様なローレンツ変換を使った事から
軸方向の寸法が縮む」という理論も、この様なローレンツ変換を使った事から
生じる誤りである事は明白でしょう。
次は、この問題を球面波という観点から見直して見ましょう。
アインシュタインは球面波と剛体の球とを混同しています。
光の球面波の式とは
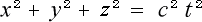
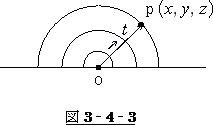 (3-4-10)
(3-4-10)
という物でローレンツ変換を作る時の土台となる式です。
光が球面波で伝わる時、その波面の任意の点を
P( 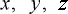 ) とすれば、上式が成り立つというものです。
) とすれば、上式が成り立つというものです。
そして剛体の球の表面の式は
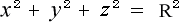
です。これは球面波の式の一歩手前の式で、光が走る所のO点からP点までの距離の式
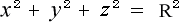
と全く同じ形をしています。従って混同はします。
剛体の球の表面を表わす式も、光の球面波の式もどちらも球面の式です。
その上、ローレンツ変換の 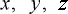 は光の球面波の
は光の球面波の 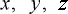 です。
です。
だから混同してしまいます。
しかしながら、両者は基本的に別物です。
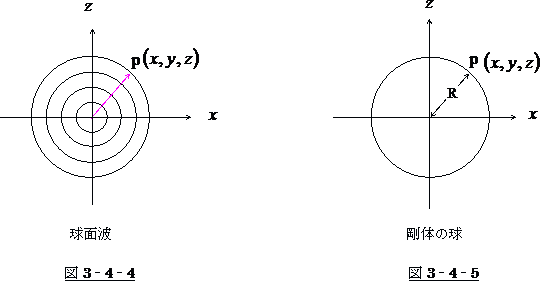
球面波は時間と共に大きくなり最後は無限大になります。
それに比べて剛体の球は剛体ですから、時間では径は変動しません。
そういう事ですから、剛体の球の式にローレンツ変換を代入する事は間違いなのです。
そんな事をして《半径が縮む》などという結論を得ても自慢にはなりません。
単に、間違っているだけですから。
ここで話を元に戻し、 =0を代入する問題に戻りましょう。
=0を代入する問題に戻りましょう。
アインシュタインは、 に0 を代入すれば不都合な
に0 を代入すれば不都合な  項が消えるとして、安易に0 を代入しました。
項が消えるとして、安易に0 を代入しました。
しかしこれは、彼が自分の創った式の意味を理解していない事を暴露しています。
 =0 という事は、ローレンツ変換では、まだ光が発されていない状態を意味しているのです。
=0 という事は、ローレンツ変換では、まだ光が発されていない状態を意味しているのです。
この時、光はまだ原点の中にあります。
従って球面波 (光の到達点) の各座標は  =0,
=0, 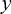 =0,
=0, 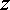 =0,
=0,  =0,
=0, 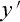 =0,
=0, 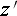 =0です。
=0です。
そうすると、本文の様に「静止系の時刻  =0 の瞬間に、この方程式を静止系から見れば」等と
=0 の瞬間に、この方程式を静止系から見れば」等と
やっても意味なくなります。
 =0 の瞬間に式(3-4-6)
=0 の瞬間に式(3-4-6)
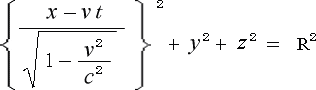
をS系より見れば
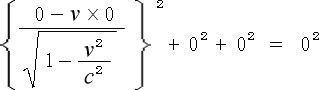
となって、全ての座標が0になり計算不能になってしまいます。
この状態では3軸の長さを求める式等出て来ません。
当然の事ながらS系とU系との長さの比も出て来ません。
「それでは、まずい」と  ≠0 にすれば、今度は
≠0 にすれば、今度は 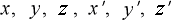 が時間と共に変動
が時間と共に変動
してしまい、剛体の球の半径が時間と共に膨張して困った事になります。
どっちにしてもアインシュタインの計算は成り立ちません。
そういう事ですから「静止系から見れば、動いている剛体の球の  軸方向の長さが縮む」という
軸方向の長さが縮む」という
理論も誤りになります。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る
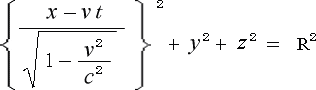
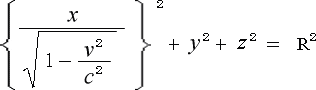 (3-4-2)
(3-4-2)