まず、図1‐4‐1の様な直交座標系を考えます。
この座標系のある点 Ｐ(
) に原点 Oより光が走ったとしましょう。
（四）数式の問題
第二節の「列車の中の時間の矛盾」の所では、光の方向によって時間が遅れたり進んだりする事を
指摘しましたが、この程度の事では相対論の先生方はビクともしないでしょう。
「あの“時間の式”は、お前が勝手にデッチ上げた物ではないか。本物の相対論では、そんな幼稚
な事はしていない。もっと高度な式が使われているのだ。あんな物でどんな結果を出した所で、
こっちの知った事ではない。相対論とは関係ない。」とやられるのが落ちでしょう。
もっとも、あのやり方は私の独自の案ではなく、講談社発行「現代物理の世界－Ⅰ 相対性理論と
量子力学の誕生」の中にある第七章「時計のパラドックス」のやり方を、そっくりそのまま真似て、
反対の結果を導き出しただけなのですけど。
それはまあ、ともかく、こうなる可能性が大ですので、相対論の誤りを指摘するには、本物の式は
欠かせません。
相対論の誤りは、数式の意味の勘違いから来ているのです。 が、何をどの様に勘違いしたのか、
それを解(わか)ってもらうには、数式の意味を知っていただく必要があります。
ここにこそ、真の原因があるからです。
そこで、ここでは、相対論の式を導く過程を通して、何が問題であるのかを説明して行く事にします。
取り敢えずは、私が大学で習った所の式の建て方に従い、ごく単純な式だけを用いて説明する事に
しましょう。
まず、図1‐4‐1の様な直交座標系を考えます。
この座標系のある点 Ｐ( ) に原点 Oより光が走ったとしましょう。
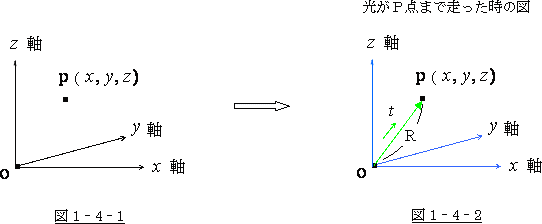
その距離 Ｒ は光速を 
、所要時間を 
として
(1-4-1)
で求まります。
次に、O P 間の距離 Ｒ の二乗をピタゴラスの定理より求めますと
(1-4-2)
となります。
（注：何でこうなるのかは、今は、考えないで下さい。
「二、式の誤りの続き」の所で出てきますから）。
そこで (1-4-1)，(1-4-2) の二式よりＲを消去して
(1-4-3)
と置きます。が、これをちょっと細工して
(1-4-4)
として置きましょう。
次に、ここに新しい座標系 
（運動undouの頭文字）を考えます。
前の系は、静止していたので Ｓ系（静止seishiの頭文字）とします。
注；Ｓ系・Ｕ系は私が勝手に付けた名で、相対論本来の呼び名ではありません。
本来はK系・K´系となっていたのですが見分けがつきにくいので、勝手に変えました
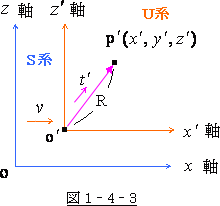系 は Ｓ系 に対して、速度 
で 
軸方向を右に動いている
物とします。
その上で、 系 でも Ｓ系 と同様にして光の走った所の距離と
時間の関係式を求めてみましょう
そうすると、それは
(1-4-5)
となるはずです。
ところで、 系の原点 O′を発した光が 系のＰ′点まで走る様子を、Ｓ系より見たらどう見える
でしょうか。
それは、図1‐4‐4（緑色の線）の様になり、
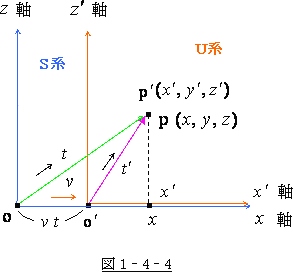その式は
(1-4-6)
となります。
そうすると、一見、無関係の様に見えていた(1-4-4),
(1-4-5) の二式も、実は、同じ光の動きを Ｓ系・ 系
という異なる立場で見た物だという事が解って来ます。
(参照図)
だとしたら、この二つの式を並べて連立方程式
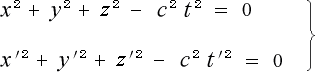(1-4-7)
にし、これを解いても誰にも文句は言われないでしょう。
そこで、これを解くわけですが、このままでは解けませんので条件に
(1-4-8)
をつけて解く事にします。
なぜ、こういう条件をつけるのかという事は、問わないで下さい。教科書に
あるのをそのまま写しているだけですから。
（ 途 中 計 算 省 略 ） 詳しくはこちら
結果
(1-4-9)
が得られます。
これが世に言うローレンツ変換です。
ところで、ここで、よく問題とされるのが、このローレンツ変換の分母の √￣￣ の中です。
系の速度 が光速 と同じになると分母が ０ になり 
や 
が無限大になります。
そして が を超えると √￣￣ の中がマイナスになり や が虚数になってしまいます。
そこで「それは困る、現実に存在する距離や時間が無限大になったり虚数になったりしては困る。
これは、いかなる物も光速を超えられないという事なのだ」という解釈が生まれて来たわけです。
しかし、ちょっと待って下さい。ここには重大な見落としが有るのです。
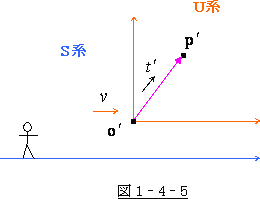
系 の速度が光速を超えるとどうなるのか、
図1‐4‐5をよく見て下さい。
系 の速度 が光速 を超えると、 系の原点 O′
を発した光が 系 のＰ′点に届いたとしても、それを
Ｓ系から見る事はできません。
なぜなら 系 そのものが光速以上の速さで遠ざかって
いるからです。見方を変えれば、それは、Ｓ系 の観測者が 系 から光速以上の速さで遠ざかって
いるのと同じ事になります。
この状態では 系 より発したいかなる光も Ｓ系 には届きません。
従って、Ｓ系 の観測者には 系 は見えません。 つまり、この状態では 系 は存在しないも
同然となるのです。 この状態では、相対論を導く為の前提がなくなります。
次に見方を変えて、Ｓ系 の原点 O を発した光が、 系 に向かっているという状況で考えてみま
しょう。
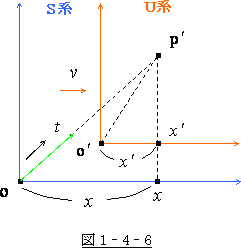
系 の速度が光速を超えていたなら、Ｓ系 の原点 O を発
した光は 系 の Ｐ′点には永久に届きません。
追いつかないからです。
追いつかなければ（1-4-7) の連立方程式は成立しません。
連立方程式が成立しなければ、相対論も成り立たなくなり
ます。つまり、これより先では相対論は無効となるのです。
要するに相対論が成り立つ為には、系の速度が光速以下で
ある事が“絶対必要条件”だったわけです。
「いかなる物も光速を超えられない」のではなく「超えたら、連立方程式が成り立たなくなり、
相対論が崩壊する」というのが真の意味だったのです。
Ｓ系 の O 点を発した光が 系 の Ｐ′点に永遠に届かなければ、距離の や時間の
が無限大になるというのは当然でしょう。
永遠に届かない（つまり無限の遠方にある）のですから。
また、速度 が光速を超えた時点で や が虚数になるというのも当然でしょう。
この連立方程式を満足させる実数解が無いのですから。
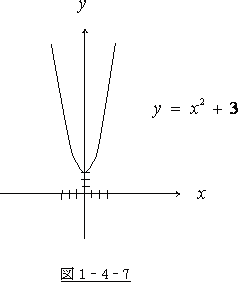
これは高校一年程度の数学の知識があればわかる事です。
二次方程式 
のグラフを書いてみれば、す
ぐにわかります。
グラフは永久に 軸には到達しません。
従って 
の時の実数解など存在しません。
これを数学で無理に解くと
となり √￣ の中がマイナスになり、虚数が出て来ます。
数式が虚数になるとは、こういう事でしょう
相対論の虚数の問題とは、実は、こういう程度の事だったのです。
なお、ここで、図1‐4‐6から見て や が虚数や無限大になっても、 や が虚数や無限
大にならなければ、関係ないではないかと、思われる方があるかも知れませんので、つけ加えておき
ます。
ローレンツ変換には、逆変換というものもあります。
それは
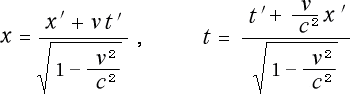（1-4-10）
というものでして、分母に関しては、正変換と全く同じ形です。
したがって、運動系の速度 が光速 と同じになれば、分母は無限大になり、距離の や時間
の も無限大になります。そして、速度 が光速 を超えれば、分母は虚数になります。
ゆえに、 や も虚数や無限大になります。
上の方で“動いている系の速度が光速を超えると連立方程式が成り立たなくなり、相対論が崩壊する”
と述べました。そして“相対論が成り立つには、系の速度が光速以下である事が絶対必要条件である”
とも述べました。
多くの人は、式を解いた結果「いかなる物も光速を超えられないのだ」と判断したのですが、実は、
そうではなかったのです。
これは、式を設定した段階で、そうなる事が義務づけられていたのです。
アインシュタインは“光速度不変の原理”という説を建てました。
それは“動いている系から見ても、静止している系から見ても、光の速度は同じ”という物です。
従来の考え方なら、動いている物から発された光の速度は「光の速度」＋「物の速度」で
； 動いている物から発された光を外から見た時の光速のベクトル表示
； 動いている物から見た光の速度のベクトル表示
； 動いている物の速度のベクトル表示
だったのですが、アインシュタインは、これを ｜｜＝｜｜ としました。
その結果 
の合成速度の大きさが となり、上限が光速に抑えられてしまったのです。
光と物の合成速度ですら光速止まりなのですから、況んや他の物の速度をや、単独の速度が光速
を超えられないのは当然でしょう。
超えてはならないのです。
最初から、そうなる様に条件をつけて式を建てているのですから。
結果がそうなって当然だったのです。
決して式を解いた結果、そうなったわけではありません。
また、合成速度の式にしても、難しい式をこねまわして
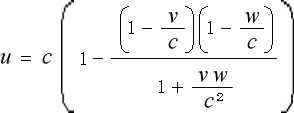(1-4-11)
などという難しい式を導き出す必要は有りませんでした。
最初から、「光速度不変の原理」で合成速度の上限を光速に抑えていたのですから。
つまり“単独の速度も合成速度も光速を超えてはならない”というのは、最初からそう決められ
ていたからなのです。
そして、それを義務づけたのが「光速度不変の原理」でした。
しかして「光速度不変の原理」には何の根拠も有りません。
誰も実験していないのですから。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る