で動いている。 次にアインシュタインは、“動いている物体の長さが縮む”という説を次の様にして導き出しました。
（イ） 原文では
「半径Ｒの剛体の球を考えよう。この球は“運動している系”に対しては静止しており、球の中
心は“運動している系”の座標原点に固定されている。
これは静止系に対しては、速度 で動いている。
その表面を表す方程式は
(3-4-1)
静止系の時刻 
＝ ０ の瞬間に、この方程式を静止系から見れば
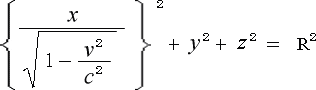(3-4-2)
この式を見れば分かる様に、静止状態では球の形をしている剛体でも、走っている状態では
−（静止系から眺めれば）− ３軸の長さが
(3-4-3)
という回転楕円体の形になる。
従って 
軸方向の長さは １：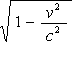 
の割合で縮んで見える。」
となっています。 (原文はこちら)
これも、何を言っているのか、さっぱり解からないと思われますので補足して説明します。
これは、剛体の球が動いている時、それを静止系から見ればどう見えるかと言う話です
半径Ｒの剛体の球の表面を表わす式は
(3-4-4)
ですが、これが
(3-4-1)
とギリシャ文字になっている理由は、アインシュタインが運動系の座標をギリシャ文字で表わしたからです。
これは同じ球の表面の式でも、運動系にある球の表面の式だという意味なのです。
(3-4-1) 式を教科書風の相対論の式で書き直せば
(3-4-5)
(注；ギリシャ文字ではわかりにくいので教科書風に書き換えました)
となります。この式の 
にローレンツ変換（1-4-9)
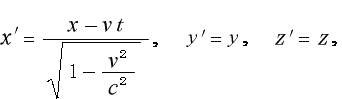
を代入すれば、(3-4-5)式は
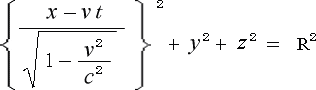(3-4-6)
となりますが、これに t ＝０を代入すれば
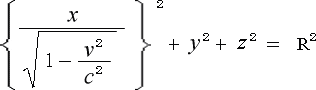
となり、本文の (3-4-2) 式 が出て来るというわけです。
次は、この式より 軸方向、
軸方向、
軸方向の、球の中心から表面までの長さを求めて見ましょう。
まず、 軸方向ですが、その為には 式 (3-4-2) に ＝０, ＝０を代入します。
｛ 理由；原点 O を中心とする球を x 軸が横切る所の座標は (x, 0，0) だから ｝
そうすると、式は
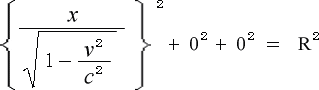(3-4-7)
になりますので、ここより
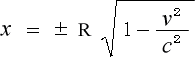(3-4-8)
が得られます。
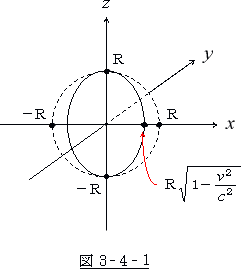同様にして 軸方向、 軸方向は共に半径 Ｒ が得られます。
その結果、三軸の長さは
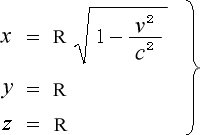(3-4-9)
となり「動いている球は静止系から見ると 軸方向の長さが
１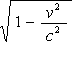： の割会で縮んで見え、回転楕円体の形になる。」
と言ってるわけです。
これは「動いている物体は、その進行方向の長さが縮んで見える」という説の元の論文です。
これも何の気無しに読むと、うっかり信じさせられます。
しかし、これも間違っています。
次へ 頁の頭に戻る 前頁に戻る HOMEに戻る